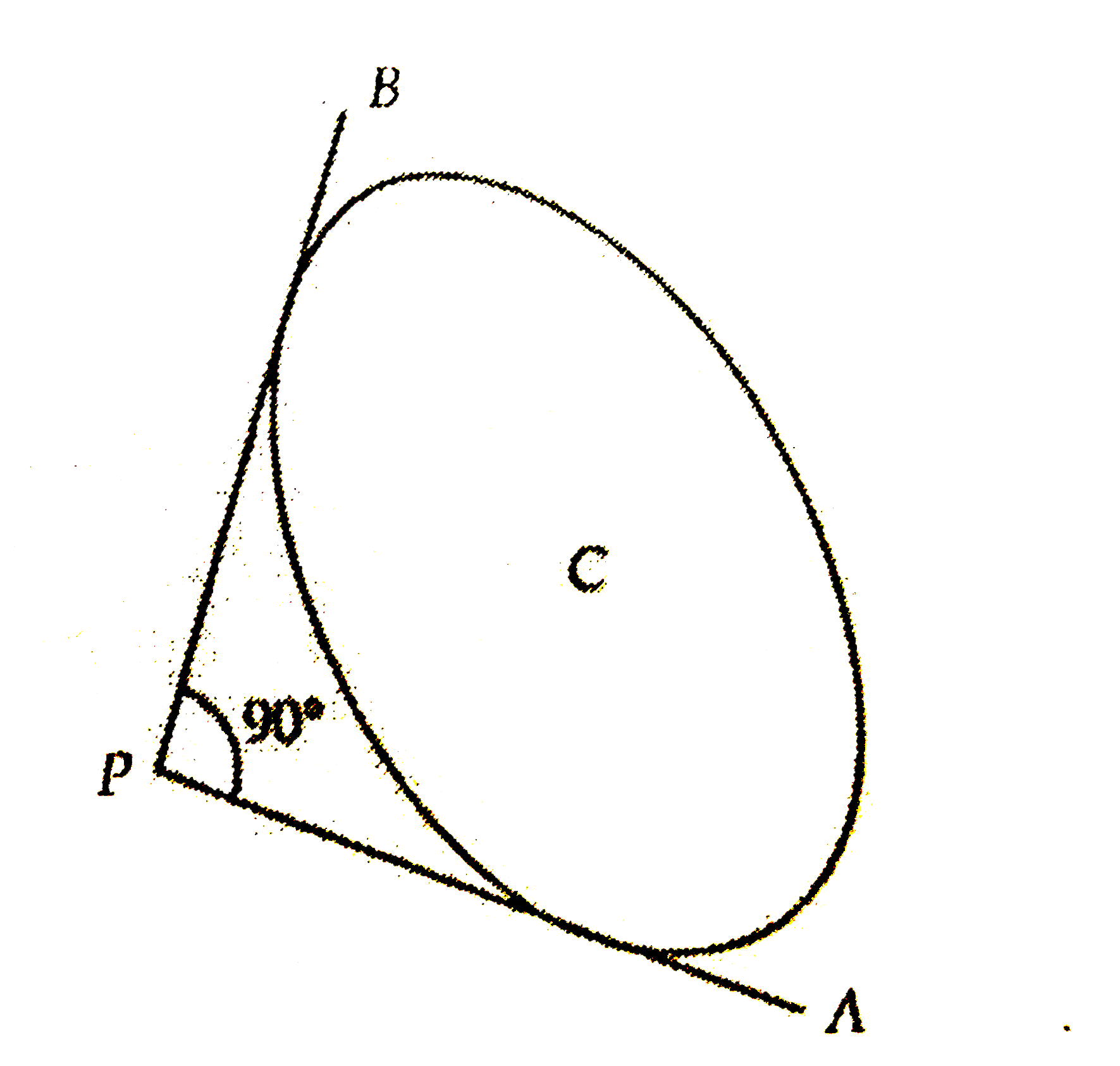
An ellipse slides between two perpendicular straight lines. Then identify the locus of its center.
parabola
ellipse
hyperbola
circle
The correct Answer is:D
Clearly, P is the point of intersection of perpendicular tangents. So, P lies on the director circle of the given ellipse (say). This means that the centre of the ellipse will always remain at a constant distance from P. Hence, the locus of C is a circle.
Topper's Solved these Questions
- ELLIPSEBook:OBJECTIVE RD SHARMA ENGLISHChapter:ELLIPSEExercise:Section II - Assertion Reason Type
Explore 7 Videos
- ELLIPSEBook:OBJECTIVE RD SHARMA ENGLISHChapter:ELLIPSEExercise:Exercise
Explore 80 Videos
- ELLIPSEBook:OBJECTIVE RD SHARMA ENGLISHChapter:ELLIPSEExercise:Chapter Test
Explore 29 Videos
- DIFFERENTIATIONBook:OBJECTIVE RD SHARMA ENGLISHChapter:DIFFERENTIATIONExercise:Chapter Test
Explore 30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBook:OBJECTIVE RD SHARMA ENGLISHChapter:EXPONENTIAL AND LOGARITHMIC SERIESExercise:Chapter Test
Explore 20 Videos
Similar Questions
An ellipse of semi-axes a,b slides between two perpendiuclar lines. Prove that the locus of its foci is (x2+y2)(x2y2+b4)=4a2x2y2, the two lines being taken as the axes of coordinates.
View SolutionA line of fixed length a+b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of length aandb is (a) an ellipse (b) parabola (c) straight line (d) none of these
View Solution
Knowledge Check
A line of length a+b moves in such a way that its ends are always on two fixed perpendicular straight lines. Then the locus of point on this line which devides it into two portions of length a and b ,is :
AA. ParabolaBB. CircleCC. EllipseDD. Hyperbola
If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
View SolutionA rod of length l slides with its ends on two perpendicular lines. Find the locus of its midpoint.
View SolutionA rod of length l slides with its ends on two perpendicular lines. Find the locus of its midpoint.
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionAn iron rod of length 2l is sliding on two mutually perpendicular lines . Find the locus of the midpoint of the rod.
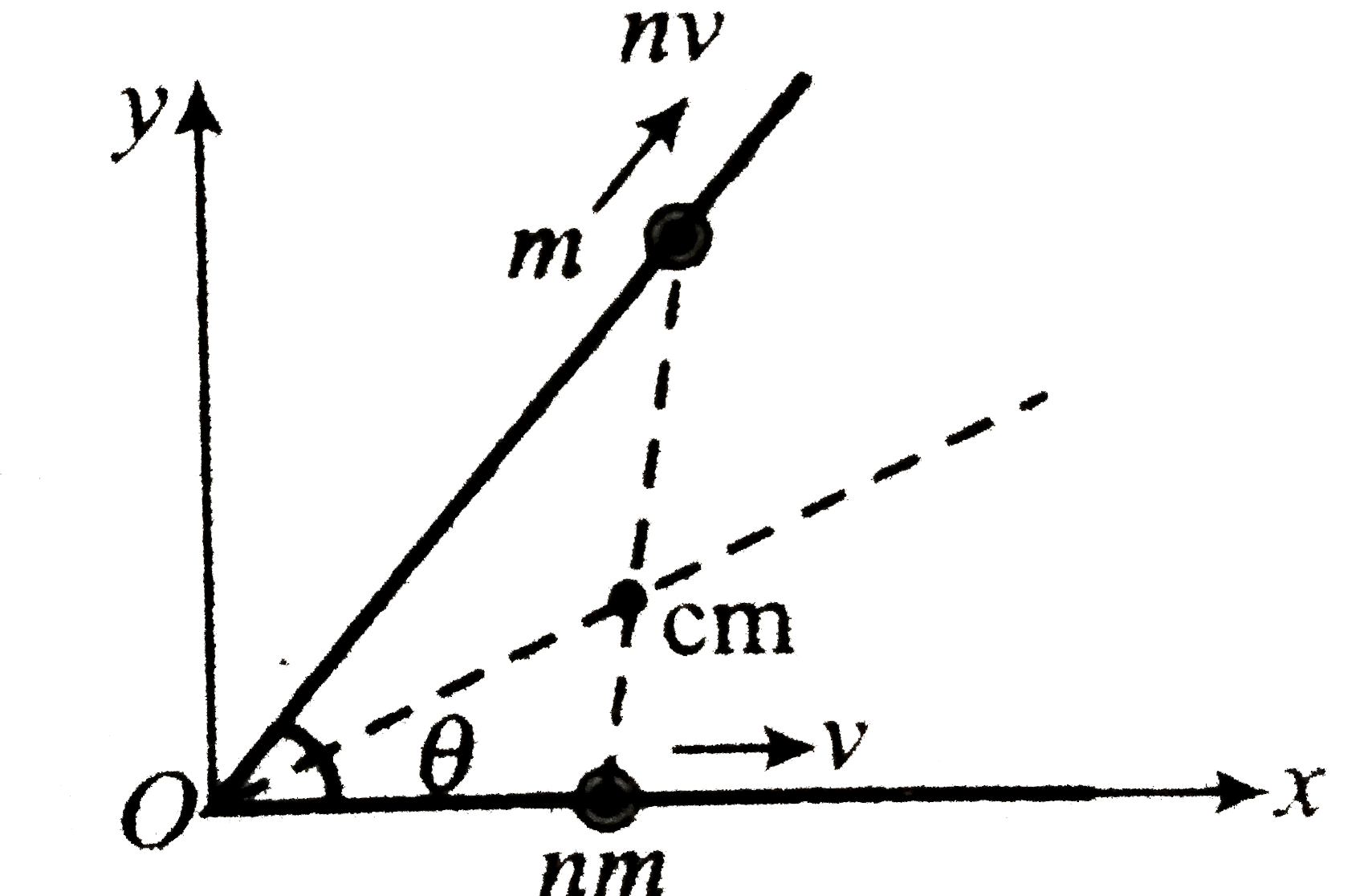
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
View SolutionA circle cuts two perpendicular lines so that each intercept is of given length. The locus of the centre of the circle is conic whose eccentricity is
View Solution
