The least value of p for which the two curves arg z=π6and∣∣z−2√3i∣∣=p intersect is
√3
3
1/√3
1/3
The correct Answer is:B
The equation ∣∣z−2√3i∣∣=p represents a circle of radius p having center at C(0,2√3) and arg(z) =π/6 is a line making an angle of 30∘ with OX and lying in first quadrant
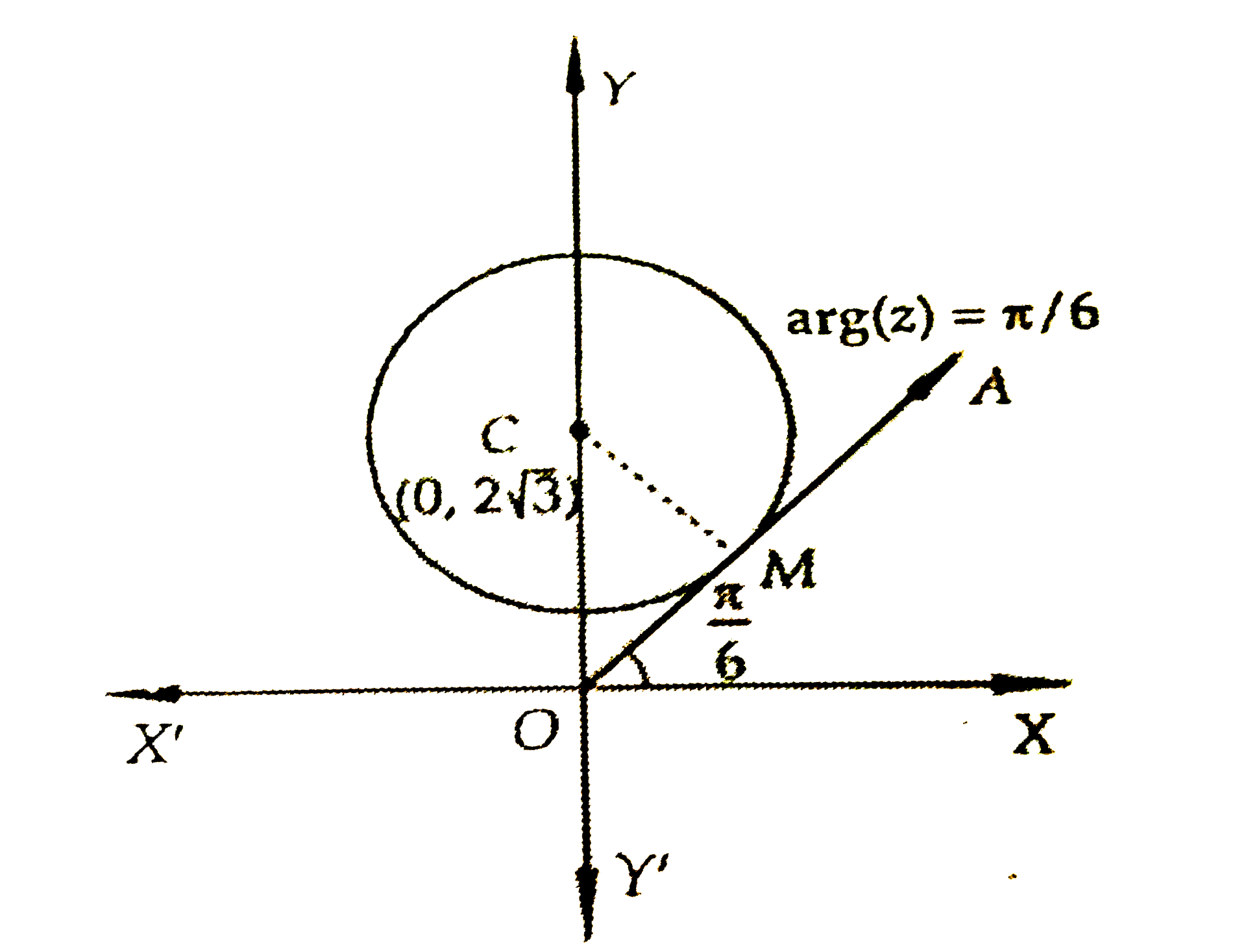
Let CM be perpendicular from C on OA. Then,
CM=OCsinπ3=2√3×√32=3
Clearly, the two curves will intersect, if
CM≤p⇒3≤p⇒p≥3.
Hence, the least value of p is 3.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section I - Solved Mcqs
141 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
The least value of p for which the two curves argz=π6 and ∣∣z−2√3i∣∣=p intersect is
View SolutionGiven that the two curves arg(z)=π6and∣∣z−2√3i∣∣=r intersect in two distinct points, then a. [r]≠2 b. 0<r<3 c. r=6 d. 3<r<2√3 (Note : [r] represents integral part of r)
View SolutionThe area bounded by the curves argz=π3andargz=2π3andarg(z−2−2i√3)=π in the argand plane is (in sq. units)
View SolutionFind the value of z, if |z|=4andarg(z)=5π6.
View SolutionThe sum of the least and greates in absolute value of z which satisfies the condition ∣∣2z+1−I√3∣∣=1, is
View SolutionLeast value of |z−2|+|z−4i| is
View SolutionThe mirror image of the curve arg(z−3z−i)=π6,i=√−1 in the real axis
View Solutionif arg(z+a)=π6 and arg(z−a)=2π3 then
View SolutionIf |z−(4+3i)|=1, then find the complex number z for each of the following cases:
(i) |z| is least
(ii) |z| is greatest
(iii) arg(z) is least
(iv) arg(z) is greatest
View SolutionLet the complex numbers z of the form x+iy satisfy arg(3z−6−3i2z−8−6i)=π4and|z−3+i|=3. Then the ordered pairs (x,y) are (A) (4−4√5,1+2√5) (B) (4+5√5,1−2√5) (C) (6−1) (D) (0,1)
View Solution
