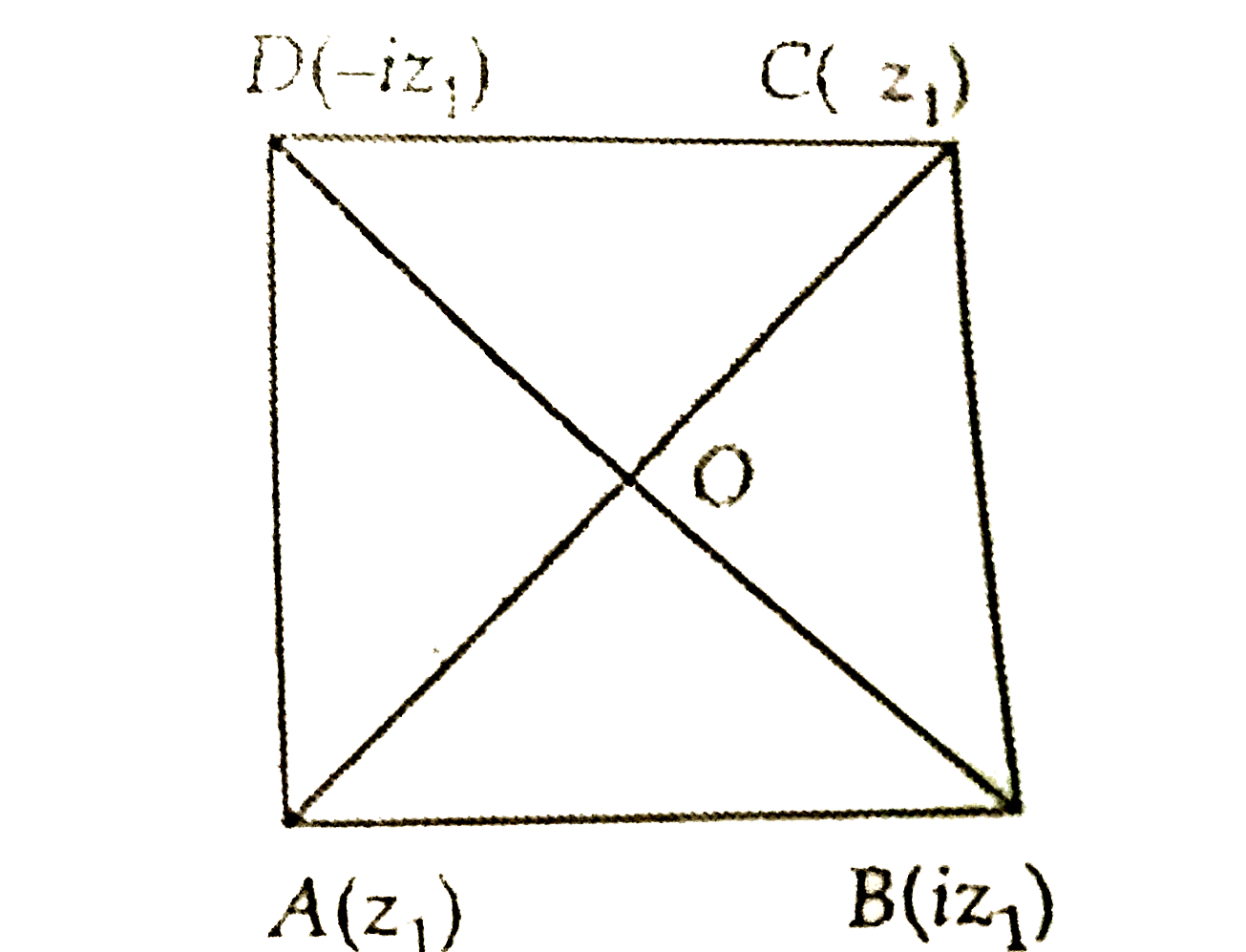
The center of a square ABCD is at the origin and point A is reprsented by z1. The centroid of △BCD is represented by
z13
−z13
iz13
−iz13
The correct Answer is:B
The affixes of the vertices B,C and D are iz1,z1 and −iz2 respectively. Therefore, the affix of the centroid of △BCD is iz1−z1−iz13=−z13
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
129 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
The centre of a square ABCD is at z=0, A is z1. Then, the centroid of △ABC is (where, i=√−1)
View SolutionThe center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.
View SolutionThe center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.
View SolutionThe center of a square is at the origin and its one vertex is A(3,2). Find the coordinates of the other vertices of the square.
View SolutionThe centre of a square ABCD is at z0. If A is z1 , then the centroid of the ABC is 2z0−(z1−z0) (b) (z0+i(z1−z03) z0+iz13 (d) 23(z1−z0)
View SolutionIf ΔOAB is an equilateral triangle (O is the origin and A is a point on the x - axis) , then centroid of the traignle will be
(a point P (x,y) is said to be rational if both x and y are rational )
View SolutionIf the circumcenter of an acute-angled triangle lies at the origin and the centroid is the middle point of the line joining the points (a2+1,a2+1) and (2a,−2a), then find the orthocentre.
View SolutionIf the circumcenter of an acute-angled triangle lies at the origin and the centroid is the middle point of the line joining the points (a2+1,a2+1) and (2a,−2a), then find the orthocentre.
View SolutionIf z1,z2,z3 be the vertices A,B,C respectively of an equilateral trilangle on the Argand plane and |z1|=|z2|=|z3| then (A) Centroid oif the triangle ABC is the complex number 0 (B) Distance between centroid and orthocentre of the triangle ABC is 0 (C) Centroid of the tirangle ABC divides the line segment joining circumcentre and orthcentre in the ratio 1:2 (D) Complex number representing the incentre of the triangle ABC is a non zero complex number
View SolutionThe center of a regular polygon of n sides is located at the point z=0, and one of its vertex z1 is known. If z2 be the vertex adjacent to z1, then z2 is equal to _____________.
View Solution
