Consider the following propositions :
P : It rains ,q : Then street gets flooded.
the propostion " If it does not rain, then the street not get flooded," is represented by
p→~q
~p→q
p↔q
~p→~q
The correct Answer is:D
To solve the problem, we need to analyze the given propositions and the statement we want to represent symbolically.
1. Identify the Propositions:
- Let P: It rains.
- Let Q: The street gets flooded.
2. Understanding the Statement:
- The statement we need to represent is: "If it does not rain, then the street does not get flooded."
- This can be broken down into its components:
- "It does not rain" is the negation of P, which we denote as ¬P.
- "The street does not get flooded" is the negation of Q, which we denote as ¬Q.
3. Formulating the Conditional Statement:
- The statement "If it does not rain, then the street does not get flooded" can be expressed in logical terms as:
¬P→¬Q
- Here, → is the conditional operator, indicating "if... then...".
4. Conclusion:
- Therefore, the proposition "If it does not rain, then the street does not get flooded" is represented by ¬P→¬Q.
Final Answer:
The proposition is represented by ¬P→¬Q.
---
- Let P: It rains.
- Let Q: The street gets flooded.
- The statement we need to represent is: "If it does not rain, then the street does not get flooded."
- This can be broken down into its components:
- "It does not rain" is the negation of P, which we denote as ¬P.
- "The street does not get flooded" is the negation of Q, which we denote as ¬Q.
- The statement "If it does not rain, then the street does not get flooded" can be expressed in logical terms as:
¬P→¬Q
- Here, → is the conditional operator, indicating "if... then...".
- Therefore, the proposition "If it does not rain, then the street does not get flooded" is represented by ¬P→¬Q.
The proposition is represented by ¬P→¬Q.
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Solved MCQs
5 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Section II - Assertion Reason Type
3 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - illusration 3
1 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
Similar Questions
Consider the following propositions
p : it rains , q : The street gets flooded.
The proposition " If it does not rain, then the street does not get flooded" is represented by
View SolutionConsider the following propositions :
P : I take medicine , q : I can sleep
Then , the compound statement ~p→~q means
View SolutionConsider the following statements
P : I have the raincoat q : I can walk in the rain.
The propositions " If i have the raincoat , then I can walk in the rain " is represented by
View SolutionConsider the following reaction , the compounds P and Q are respectively
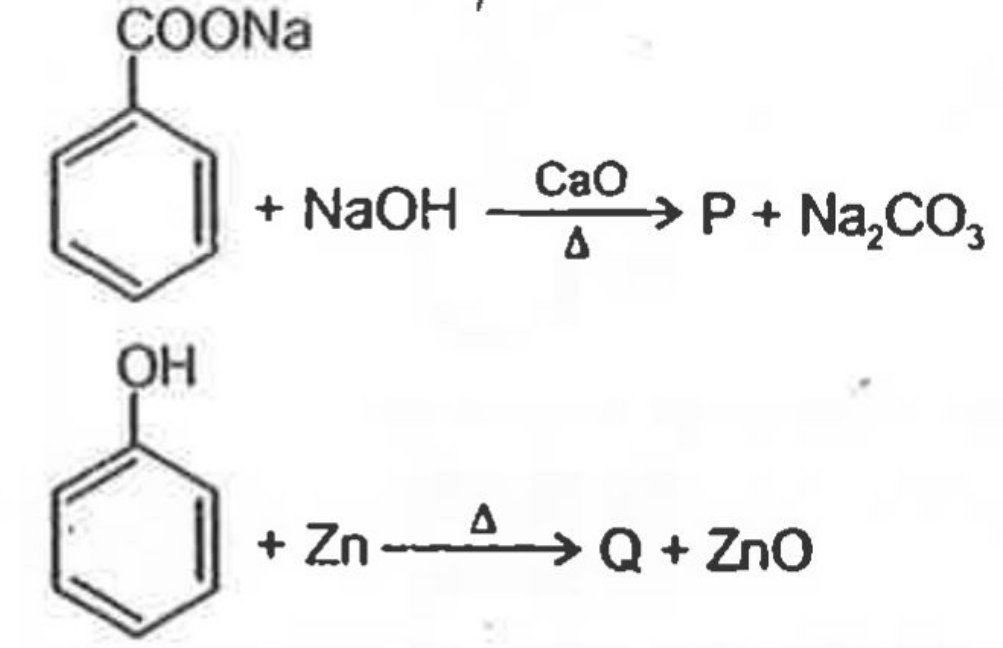
View SolutionConsider the following statements:
p : I shall pass, q : I study
The symbolic represention of the proposition " I shall pass iff I study" is
View SolutionConsider the following reaction sequence

The compounds P and Q are :
View SolutionWhich of the following is true for the propositions p and q ?
View SolutionWrite the following statements in the form if p then q: It never rains when it is cold.
View SolutionWrite the following statement in the form if p then q: It rains only if it is cold.
View SolutionConsider the following statement :
p : I shall pass, q : I study, then write the verbal translation of the symbolic representation p⇔q.
View Solution
