which of the following is a contradiction ?
(p∧q)∧(~p∧~q)
p∨~q
~p∧q
~p∧~q
To determine which of the given statements is a contradiction, we need to analyze each option using truth tables. A contradiction is a statement that is always false, regardless of the truth values of its components.
1. Identify the Variables:
Let p and q be the two variables involved in the statements.
2. Construct the Truth Table:
We will create a truth table that includes all possible combinations of truth values for p and q. The truth values can be either True (T) or False (F).
| p | q | ¬p | ¬q |
|---------|---------|---------------|---------------|
| T | T | F | F |
| T | F | F | T |
| F | T | T | F |
| F | F | T | T |
3. Evaluate Each Option:
We will evaluate each option to see if it results in a contradiction (i.e., all false values).
- Option 1: p∧q
- Truth Table:
| p | q | p∧q |
|---------|---------|------------------|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
- Result: Not a contradiction (not all false).
- Option 2: p∨¬q
- Truth Table:
| p | ¬q | p∨¬q |
|---------|---------------|----------------------|
| T | F | T |
| T | T | T |
| F | F | F |
| F | T | T |
- Result: Not a contradiction (not all false).
- Option 3: ¬p∧q
- Truth Table:
| ¬p | q | ¬p∧q |
|---------------|---------|-----------------------|
| F | T | F |
| F | F | F |
| T | T | T |
| T | F | F |
- Result: Not a contradiction (not all false).
- Option 4: ¬p∧¬q
- Truth Table:
| ¬p | ¬q | ¬p∧¬q |
|---------------|---------------|-----------------------------|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
- Result: Not a contradiction (not all false).
4. Final Evaluation:
After evaluating all options, we find that none of the options are contradictions. However, if we had an option that consistently resulted in all false values, that would be the contradiction.
Conclusion:
Based on the evaluations, if we had an option that consistently resulted in all false values, that would be our contradiction. In this case, if we had p∧¬p or similar, that would be a contradiction.
Let p and q be the two variables involved in the statements.
We will create a truth table that includes all possible combinations of truth values for p and q. The truth values can be either True (T) or False (F).
|---------|---------|---------------|---------------|
| T | T | F | F |
| T | F | F | T |
| F | T | T | F |
| F | F | T | T |
We will evaluate each option to see if it results in a contradiction (i.e., all false values).
- Truth Table:
| p | q | p∧q |
|---------|---------|------------------|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
- Result: Not a contradiction (not all false).
- Truth Table:
| p | ¬q | p∨¬q |
|---------|---------------|----------------------|
| T | F | T |
| T | T | T |
| F | F | F |
| F | T | T |
- Result: Not a contradiction (not all false).
- Truth Table:
| ¬p | q | ¬p∧q |
|---------------|---------|-----------------------|
| F | T | F |
| F | F | F |
| T | T | T |
| T | F | F |
- Result: Not a contradiction (not all false).
- Truth Table:
| ¬p | ¬q | ¬p∧¬q |
|---------------|---------------|-----------------------------|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
- Result: Not a contradiction (not all false).
After evaluating all options, we find that none of the options are contradictions. However, if we had an option that consistently resulted in all false values, that would be the contradiction.
Based on the evaluations, if we had an option that consistently resulted in all false values, that would be our contradiction. In this case, if we had p∧¬p or similar, that would be a contradiction.
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Section II - Assertion Reason Type
3 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
Similar Questions
which of the following is not ?
View SolutionWhich one of the following is not a contradiction? [~p∧(p∨~q)]∧q b. (~p∧q)∧p c. [(p(→)q)(→)p]∧~p d. (~q(→)~p)↔(p(→)q)
View SolutionMatch the following :

Which of the following is correct option ?
View SolutionAmongst the following mammals which of the following is a monotreme?
View SolutionIn the following reaction, which of the following steps is wrong ?
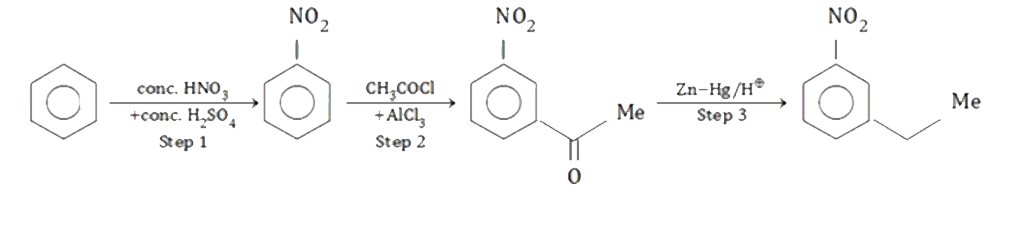
View SolutionAccording to the following diagram,which of the following option is correct ?
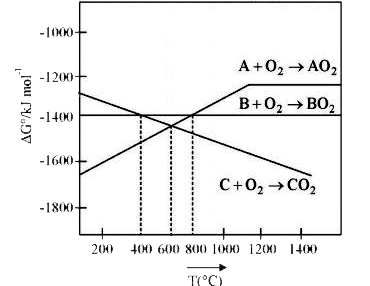
View SolutionWhich of the following is correct about the following compound
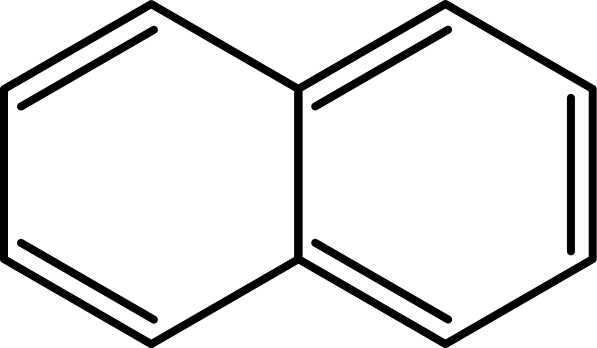
View SolutionProve the following statement by contradiction method
p The sum of in irrational number and a rational number is irrational
View SolutionFollowing graph is obsereved for which of the following electrolytic solution.
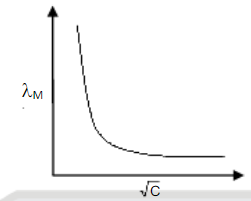
View SolutionWhich of the following is true regarding the following conformations of butane.
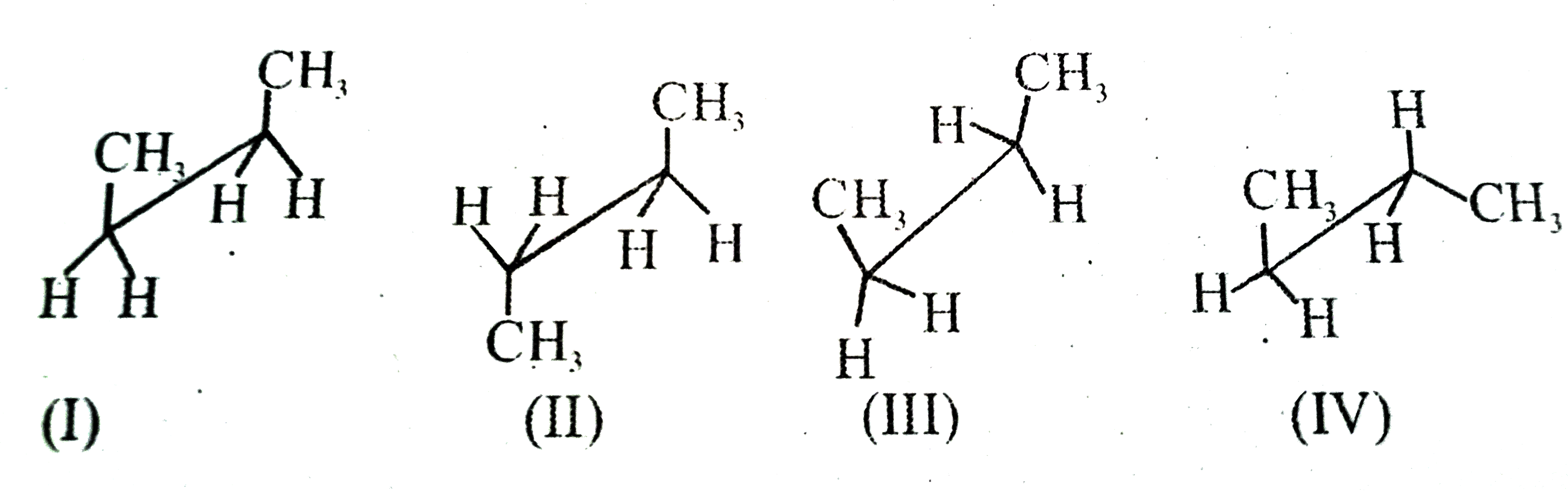
View Solution
