which of the following is a contradiction ?
p∨q
P∧q
p∨~p
p∧~p
The correct Answer is:D
To determine which of the given options is a contradiction, we will analyze each option using truth tables. A contradiction is a statement that is always false, regardless of the truth values of its components.
1. Identify the Variables: Let's denote two propositions as p and q.
2. Construct the Truth Table: We will create a truth table for p and q to evaluate the logical expressions. The truth values for p and q can be represented as follows:
| p | q |
|---------|---------|
| T | T |
| T | F |
| F | T |
| F | F |
3. Evaluate Each Option:
- Option A: p∪q (Logical OR)
- This expression is true if at least one of p or q is true.
- Truth values:
- T (T or T)
- T (T or F)
- T (F or T)
- F (F or F)
- Conclusion: Not a contradiction (true in some cases).
- Option B: p∩q (Logical AND)
- This expression is true only if both p and q are true.
- Truth values:
- T (T and T)
- F (T and F)
- F (F and T)
- F (F and F)
- Conclusion: Not a contradiction (true in one case).
- Option C: p∪¬p (Logical OR with negation)
- This expression is always true because either p is true or p is false.
- Truth values:
- T (T or F)
- T (T or F)
- T (F or T)
- T (F or T)
- Conclusion: Not a contradiction (always true).
- Option D: p∩¬p (Logical AND with negation)
- This expression is true only if both p is true and p is false, which is impossible.
- Truth values:
- F (T and F)
- F (T and F)
- F (F and T)
- F (F and T)
- Conclusion: This is a contradiction (always false).
4. Final Answer: The option that is a contradiction is Option D.
|---------|---------|
| T | T |
| T | F |
| F | T |
| F | F |
- Option A: p∪q (Logical OR)
- This expression is true if at least one of p or q is true.
- Truth values:
- T (T or T)
- T (T or F)
- T (F or T)
- F (F or F)
- Conclusion: Not a contradiction (true in some cases).
- This expression is true only if both p and q are true.
- Truth values:
- T (T and T)
- F (T and F)
- F (F and T)
- F (F and F)
- Conclusion: Not a contradiction (true in one case).
- This expression is always true because either p is true or p is false.
- Truth values:
- T (T or F)
- T (T or F)
- T (F or T)
- T (F or T)
- Conclusion: Not a contradiction (always true).
- This expression is true only if both p is true and p is false, which is impossible.
- Truth values:
- F (T and F)
- F (T and F)
- F (F and T)
- F (F and T)
- Conclusion: This is a contradiction (always false).
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Exercise
38 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
Similar Questions
which of the following is not ?
View SolutionWhich one of the following is not a contradiction? [~p∧(p∨~q)]∧q b. (~p∧q)∧p c. [(p(→)q)(→)p]∧~p d. (~q(→)~p)↔(p(→)q)
View SolutionMatch the following :

Which of the following is correct option ?
View SolutionAmongst the following mammals which of the following is a monotreme?
View SolutionRead the following statements. Which one of the following is incorrect?
View SolutionIn the following reaction, which of the following steps is wrong ?
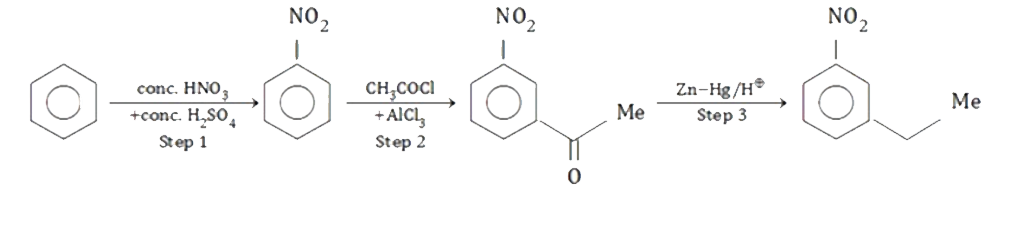
View SolutionWhich of the following is the correct order of stability of the
following compounds ?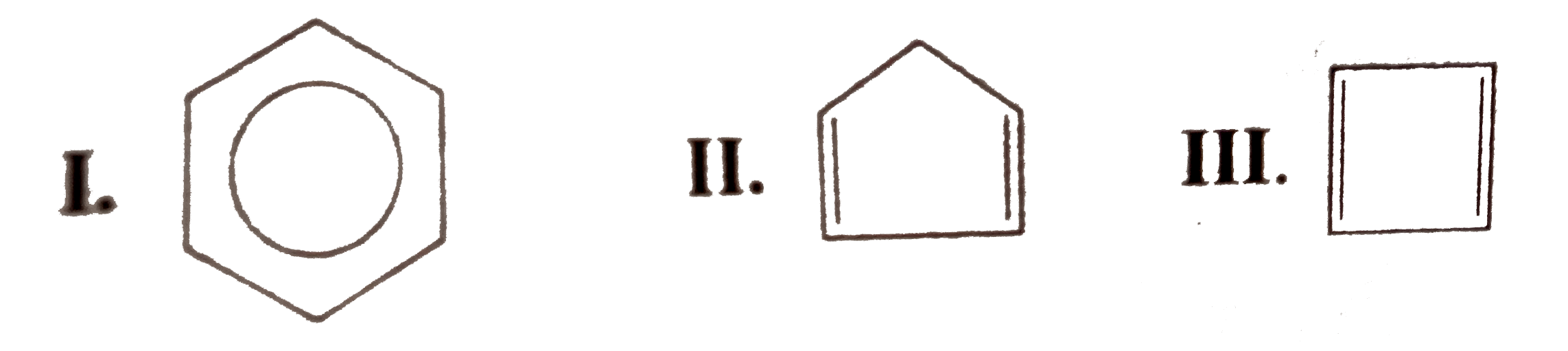
View SolutionAccording to the following diagram,which of the following option is correct ?
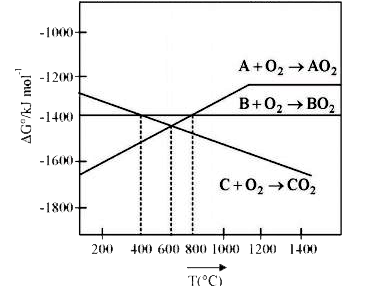
View SolutionProve the following statement by contradiction method
p The sum of in irrational number and a rational number is irrational
View SolutionFollowing graph is obsereved for which of the following electrolytic solution.
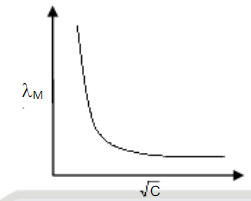
View Solution
