In a △ABC,B=π8,C=5π8. The altitude from A to the side BC, is
a2
2a
12(b+c)
b+c
The correct Answer is:A
To find the altitude from vertex A to side BC in triangle ABC, where B=π8 and C=5π8, we will use the formula for the altitude from a vertex in a triangle.
1. Identify the Angles:
- Given B=π8 and C=5π8.
- To find angle A, use the fact that the sum of angles in a triangle is π:
A=π−B−C=π−π8−5π8=π−6π8=2π8=π4
2. Use the Altitude Formula:
- The formula for the altitude hA from vertex A to side BC is given by:
hA=acotA+cotB+cotC
- We need to find cotA, cotB, and cotC.
3. Calculate Cotangents:
- Calculate cotA:
cotA=cot(π4)=1
- Calculate cotB:
cotB=cot(π8)=cosπ8sinπ8
- Calculate cotC:
cotC=cot(5π8)=cos5π8sin5π8=−cot(3π8)=−cos3π8sin3π8
4. Use Cotangent Addition:
- We can use the identity for cotangent:
cotB+cotC=cot(π8)−cot(3π8)
- This can be simplified further using known values or identities.
5. Combine Cotangents:
- Now, substitute back into the altitude formula:
hA=acot(π4)+cot(π8)+cot(5π8)
- This will yield a numerical value once a is known.
6. Final Calculation:
- If we assume a=2 (for simplicity), then:
hA=21+cot(π8)−cot(3π8)
- After evaluating the cotangent values, we can find the altitude.
Conclusion:
The altitude from A to side BC can be expressed as:
hA=acotB+cotC+1
For specific values of a, the altitude can be calculated numerically.
- Given B=π8 and C=5π8.
- To find angle A, use the fact that the sum of angles in a triangle is π:
A=π−B−C=π−π8−5π8=π−6π8=2π8=π4
- The formula for the altitude hA from vertex A to side BC is given by:
hA=acotA+cotB+cotC
- We need to find cotA, cotB, and cotC.
- Calculate cotA:
cotA=cot(π4)=1
- Calculate cotB:
cotB=cot(π8)=cosπ8sinπ8
- Calculate cotC:
cotC=cot(5π8)=cos5π8sin5π8=−cot(3π8)=−cos3π8sin3π8
- We can use the identity for cotangent:
cotB+cotC=cot(π8)−cot(3π8)
- This can be simplified further using known values or identities.
- Now, substitute back into the altitude formula:
hA=acot(π4)+cot(π8)+cot(5π8)
- This will yield a numerical value once a is known.
- If we assume a=2 (for simplicity), then:
hA=21+cot(π8)−cot(3π8)
- After evaluating the cotangent values, we can find the altitude.
The altitude from A to side BC can be expressed as:
hA=acotB+cotC+1
For specific values of a, the altitude can be calculated numerically.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Exercise
97 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
Knowledge Check
In △ABC,∠A=45∘,∠B=30∘,andb=8. Side a =
A6.5B11C12D14
If in a △ABC,A=π3andAD is the median, then
View Solution△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View SolutionA(5,−3),B(8,2),C(0,0) are the vertices of a triangle. Show that the median from A is perpendicular to the side BC.
View SolutionFind the perimeter of each of the following shapes: a) An equilateral triangle of side 9cm. b) An isosceles triangle with equal side 8cm each and third side 6cm. c) An isosceles triangle ABC, with AB=AC=10cm and altitude from A on BC equal to 8cm. d) A regular hexagon with each side measuring 8cm.
View SolutionIn a △ABC , B=(2,3),C=(7,-1) and AB=3,AC=5 then find the equation of altitude through the vertex A.
View SolutionIn △ABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. △PQR is constructed
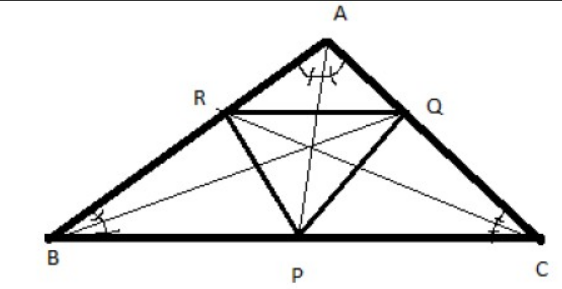
If AB=7 units, BC = 8 units, AC = 5 units, then the side PQ will be
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View Solution
