Let O, P and Z represent the numbers 0, 3 and -5 respectively on the number line. Points Q, R and S are between O and P such that OQ = QR = RS = SP.
What are the rational numbers represented by the points Q, R and S. Next choose a point T between Z and O so that ZT = TO. Which rational number does T represent?
To solve the problem step by step, we will first find the rational numbers represented by points Q, R, and S between O (0) and P (3), and then we will find the rational number represented by point T between Z (-5) and O (0).
Step 1: Determine the distances between points O, P, Q, R, S
- We know that O = 0 and P = 3.
- The distance between O and P is 3−0=3.
- We need to divide this distance into 4 equal parts since we have points Q, R, S, and the segment SP.
Step 2: Calculate the length of each segment
- Let the length of each segment be x.
- Since there are 4 segments, we have:
OQ+QR+RS+SP=3
4x=3
x=34
Step 3: Find the positions of points Q, R, and S
- Position of Q:
OQ=x=34
So, Q=0+34=34.
- Position of R:
R=OQ+QR=34+34=64=32
- Position of S:
S=OQ+QR+RS=34+34+34=94
Step 4: Choose a point T between Z and O
- We know that Z = -5 and O = 0.
- The distance between Z and O is 0−(−5)=5.
- We need to find point T such that ZT=TO.
Step 5: Calculate the length of each segment for T
- Let the length of each segment be y.
- Since there are 2 segments (ZT and TO), we have:
ZT+TO=5
2y=5
y=52
Step 6: Find the position of point T
- Since T is between Z and O, we can calculate:
T=Z+y=−5+52=−5+2.5=−2.5
Thus, T=−52.
Summary of Results
- The rational numbers represented by the points are:
- Q=34
- R=32
- S=94
- The rational number represented by point T is:
- T=−52
- We know that O = 0 and P = 3.
- The distance between O and P is 3−0=3.
- We need to divide this distance into 4 equal parts since we have points Q, R, S, and the segment SP.
- Let the length of each segment be x.
- Since there are 4 segments, we have:
OQ+QR+RS+SP=3
4x=3
x=34
- Position of Q:
OQ=x=34
So, Q=0+34=34.
R=OQ+QR=34+34=64=32
S=OQ+QR+RS=34+34+34=94
- We know that Z = -5 and O = 0.
- The distance between Z and O is 0−(−5)=5.
- We need to find point T such that ZT=TO.
- Let the length of each segment be y.
- Since there are 2 segments (ZT and TO), we have:
ZT+TO=5
2y=5
y=52
- Since T is between Z and O, we can calculate:
T=Z+y=−5+52=−5+2.5=−2.5
Thus, T=−52.
- The rational numbers represented by the points are:
- Q=34
- R=32
- S=94
- The rational number represented by point T is:
- T=−52
Topper's Solved these Questions
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Example (Problem Solving Strategies)
1 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Exercise (Choose the correct answer)
25 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Example (true or false)
2 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
Similar Questions
The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
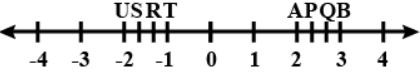
View SolutionThe points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
View SolutionIf the points P and Q represent the real numbers 0.8¯3 and 0.6¯2 on the number line, then the distance between P and Q is
View SolutionIf the points P and Q represent real numbers 0.7¯3 and 0.5¯6 on the number line, then what is the distance between P and Q?
View SolutionIn Argand diagram, O, P, Q represent the origin, z and z+ iz respectively then ∠OPQ=
View SolutionWhich rational number does the point P represent on this number line ?

View SolutionFind the vlaues of P,Q,R,S and T on the given number line.

View SolutionEvery rational number can be represented by some point on the number line, is this statement true or false?
View SolutionEvery rational number can be represented by some point on the number line, is this statement true or false?
View SolutionFind four rational numbers between 1/9 and 1/3 and represent them on the number line.
View Solution
