Volume of a rectangular box (cuboid) with length = 2ab, breadth = 3ac and height = 2ac is
12a3bc2
12a2bc
12a2bc
2ab+3ac+2ac
To find the volume of a rectangular box (cuboid) with given dimensions, we can follow these steps:
Step 1: Identify the dimensions of the cuboid
The dimensions provided are:
- Length (L) = 2ab
- Breadth (B) = 3ac
- Height (H) = 2ac
Step 2: Use the formula for the volume of a cuboid
The formula for the volume (V) of a cuboid is given by:
V=L×B×H
Step 3: Substitute the dimensions into the formula
Now, we substitute the values of length, breadth, and height into the volume formula:
V=(2ab)×(3ac)×(2ac)
Step 4: Multiply the constant terms
First, we multiply the numerical coefficients:
2×3×2=12
Step 5: Multiply the variable terms
Next, we multiply the variable parts:
- For a:
- From 2ab, we have a1
- From 3ac, we have a1
- From 2ac, we have a1
Adding the powers of a:
1+1+1=3
So, we have a3.
- For b:
- From 2ab, we have b1
- From 3ac and 2ac, there are no b terms.
So, we have b1.
- For c:
- From 3ac, we have c1
- From 2ac, we have c1
Adding the powers of c:
1+1=2
So, we have c2.
Step 6: Combine the results
Now, we can combine all the parts together:
V=12×a3×b1×c2
This simplifies to:
V=12a3bc2
Final Answer:
The volume of the rectangular box (cuboid) is:
V=12a3bc2
---
The dimensions provided are:
- Length (L) = 2ab
- Breadth (B) = 3ac
- Height (H) = 2ac
The formula for the volume (V) of a cuboid is given by:
V=L×B×H
Now, we substitute the values of length, breadth, and height into the volume formula:
V=(2ab)×(3ac)×(2ac)
First, we multiply the numerical coefficients:
2×3×2=12
Next, we multiply the variable parts:
- For a:
- From 2ab, we have a1
- From 3ac, we have a1
- From 2ac, we have a1
Adding the powers of a:
1+1+1=3
So, we have a3.
- From 2ab, we have b1
- From 3ac and 2ac, there are no b terms.
- From 3ac, we have c1
- From 2ac, we have c1
Adding the powers of c:
1+1=2
So, we have c2.
Now, we can combine all the parts together:
V=12×a3×b1×c2
This simplifies to:
V=12a3bc2
The volume of the rectangular box (cuboid) is:
V=12a3bc2
Topper's Solved these Questions
Similar Questions
Volume of a rectangular box with length 2x, breadth 3y and height 4z is _________.
View SolutionThe volume of a rectangular glass slab of length= 3 cm, breadth 2 cm and height 2 cm is____cm3
View SolutionFind the volume of each rectangular box with given length, breadth and height.
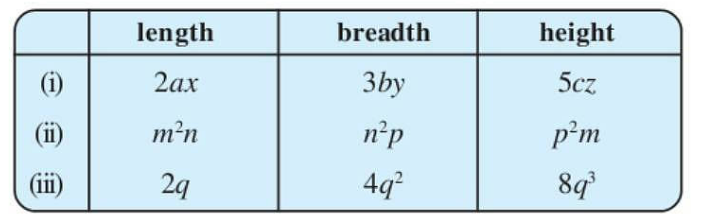
View SolutionFind the volume of a rectangular box having a length of 5 m, width of 3 m , and height of 4 m .
View SolutionFind the volume of the rectangular boxes with following length, breadth and height: Length Breadth Height 2ax 3by 5cz m2n n2p
View SolutionFind the volume and total surface area of a cuboid, whose length = 15 cm, breadth = 10 cm and height = 8 cm.
View SolutionFind the volume and total surface area of a cuboid whose length = 3.5 m, breadth = 2.6 m and height = 0.9 m.
View SolutionObtain the volume of rectangular boxes with the following length, breadth and height respectively. (i) 5a,3a2,7a4 (ii) 2p,4q,8r (iii) xy,2x2y,2xy2 (iv) a,2b,3c
View SolutionThe volume of a rectangular slab is 12cm3. The length and breadth of the slab are 3 cm and 2 cm respectively. Find its height.
View SolutionFind the volume of a cuboid whose (i) length =12 c m
View Solution
