Two identical springs, each of spring constant K, are connected first series and then in parallel. A mass M is suspended from them. The ratio of the frequencies of vertical oscillations will be :Solution in Malayalam
2:1
1:1
1:4
1:2
The correct Answer is:D
Time period of spring mass system is
T=2π√mk
When connected in series k.=k2
When connected in parallel k..=2k
∴ T.T..=√k2(2k)=12
Similar Questions
Two identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View Solutionदो स्प्रिंग जिनमे प्रत्येक का स्प्रिंग नियतांक k है पहले श्रेणी क्रम में जुड़ती है तथा बाद में समान्तर क्रम में जुड़ती है। एक m द्रव्यमान इनसे लटकाया जाता है। इनके दोलनों की आवृतियो का अनुपात होगा
View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be
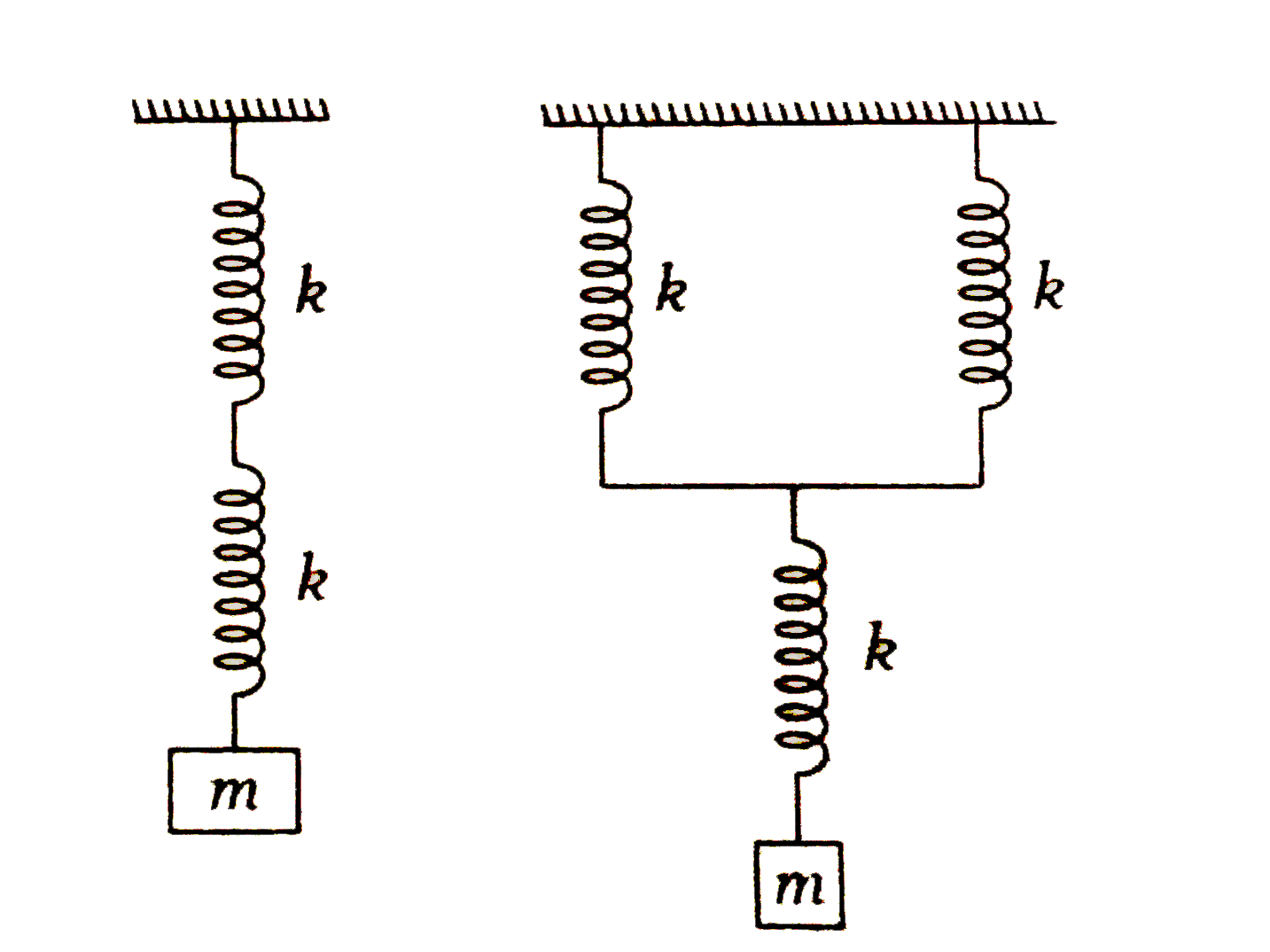
View SolutionA weightless spring which has a force constant k oscillates with frequency n when a mass m is suspended from it The spring is cut into two equal halves and a mass 2m is suspended from it. The frequency of oscillation will now become
View SolutionTwo identical springs of constant k are connected , first in series and then in parallel. A matal block of mass m is suspended from their combination. The ratio of their frequencies of vertical oscillations will be in a ratio
View Solution
