The ratio of resistances of two copper wires of the same length and of same cross-sectional area when connected in series to that when connected in parallel is
1:1
1:2
2:1
4:1
The correct Answer is:D
Let R be the resistance of copper wire. In the first condition,
Rseries=R+R=2R …(i)
In the second condition,
1Rparallel=1R+1R,1Rparallel=1+1R
Rparallel=R2 …(ii)
On dividing Eq. (i) by Eq. (ii), we get
RseriesRparallel=2RR2=41
Similar Questions
Nichrome and copper wires of same length and area of cross-section are connected in sereis, current is passed through them. Why does the nichrome wire get heated first ?
View SolutionTwo heating coils, one of fine wire and the other of thick wire of the same material and of the same length are connected in series and in parallel. Which of the following statement is correct ?
View Solution
Knowledge Check
Two heating coils, one of fine wire and the other of thick wire of the same material and of the same length are connected in series and in parallel. Which of the following statement is correct ?
AIn series fine wire liberates more energy while in parallel thich wire will liberatre more energyBIn series fine wire liberates less energy while in parallel thick liberate more energyCBoth will liberate equallyDIn series the thick wire will liberate more while in parallel it will liberate less energyTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
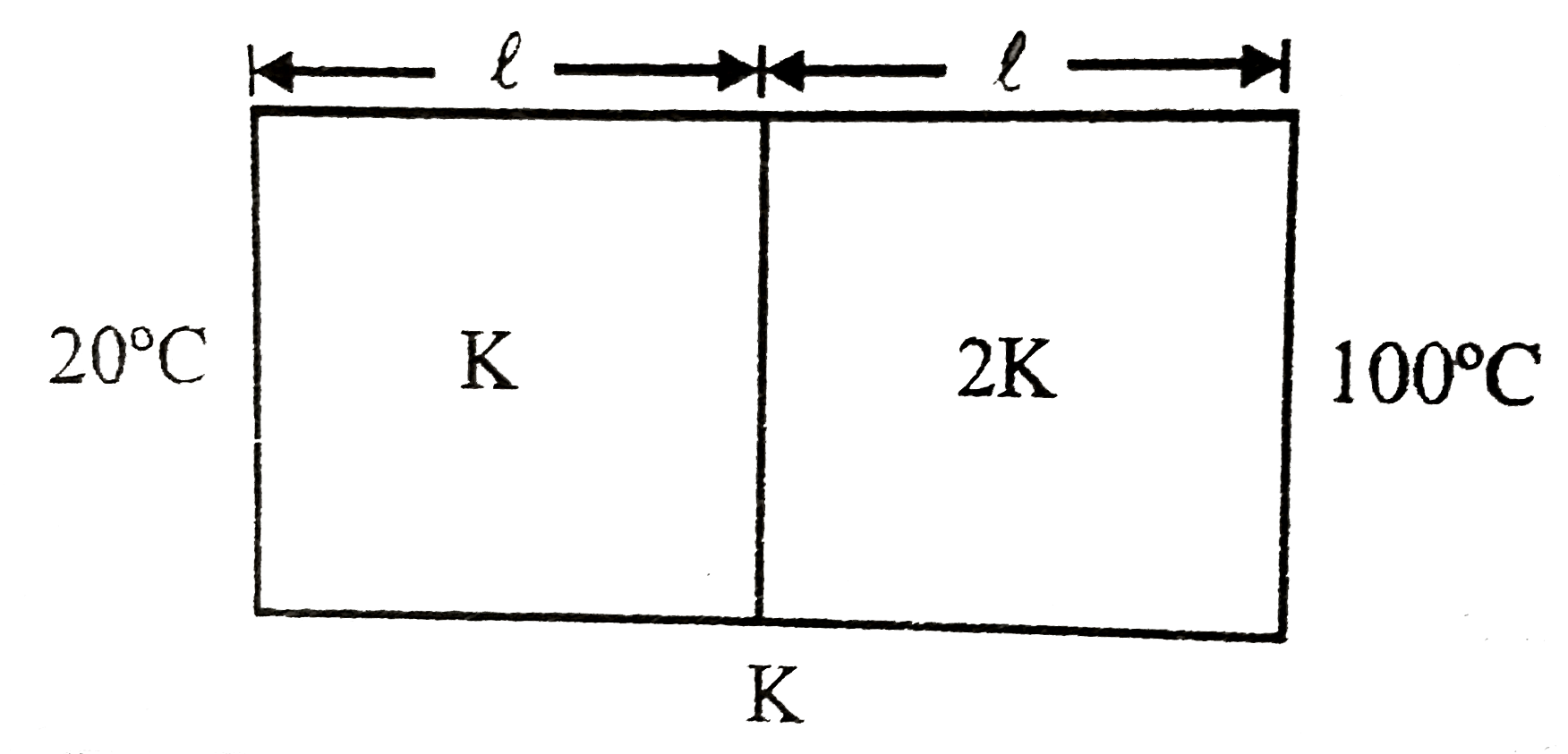 A60∘CB73.3∘CC46.7∘CD37.3∘C
A60∘CB73.3∘CC46.7∘CD37.3∘CTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
A4k1k2(k1+k2)2BnoneC(k1+k2k1−k2)Dk1k2(k1+k2)2
Two metallic wires of the same material B, have the same length out cross-sectional area is in the ratio 1:2. They are connected (i) in series and (ii) in parallel. Compare the drift velocities of electrons in the two wires in both the cases (i) and (ii) .
View SolutionTwo metallic wires of the same material B, have the same length out cross-sectional area is in the ratio 1:2. They are connected (i) in series and (ii) in parallel. Compare the drift velocities of electrons in the two wires in both the cases (i) and (ii) .
View SolutionThe resultant resistance of n wires each of resistance r ohms is R, when they are connected in parallel. When these n resistances are connected in series, the resultant resistance will be
View SolutionThe resultant resistance of n wires each of resistance r ohms is R ,when they are connected in parallel.When these n resistances are connected in series,the resultant resistance will be
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View Solution
