एक रेखाखंड ¯¯¯¯¯¯XY का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
a. इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जांच कीजिए कि PX=PY है।
b. यदि M रेखाखंड ¯¯¯¯¯¯XY का मध्य बिंदु है तो MX और XY के विषय में आप क्या कह सकते हैं?
The correct Answer is:5.15 सेमी
Step by step video, text & image solution for एक रेखाखंड bar(XY) का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है। a. इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जांच कीजिए कि PX=PY है। b. यदि M रेखाखंड bar(XY) का मध्य बिंदु है तो MX और XY के विषय में आप क्या कह सकते हैं? by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- प्रायोगिक ज्यामितिBOOK - MBD PUBLICATIONCHAPTER - प्रायोगिक ज्यामितिEXERCISE - प्रश्नावली 14.6
9 Videos
- प्रायोगिक ज्यामितिBOOK - MBD PUBLICATIONCHAPTER - प्रायोगिक ज्यामितिEXERCISE - प्रश्नावली 14.4
3 Videos
- पूर्णांक BOOK - MBD PUBLICATIONCHAPTER - पूर्णांक EXERCISE - इन्हें कीजिए
4 Videos
- प्रारंभिक आकारों को समझना BOOK - MBD PUBLICATIONCHAPTER - प्रारंभिक आकारों को समझना EXERCISE - इन्हे कीजिए
20 Videos
Similar Questions
75∘ माप वाले एक कोण ∠POQ की रचना कीजिए और इसकी सममित अक्ष खींचिए।
View Solutionएक रेखाखंड ¯¯¯¯¯¯AB खींचिएं। इस पर कोई बिंदु M अंकित कीजिए। M से होकर एक ¯¯¯¯¯¯AB पर एक लंब, रूलर और परकार द्वारा खींचिए।
View Solutionमान लीजिए डेविड और मोहन ने 0 स्थान से विपरीत दिशाओं में चलना प्रारम्भ कर दिया है। मान लीजिए कि 0 के दाईं ओर चले कदमो को + चिह्न से निरूपित किया जाता है और 0 से बाईं ओर चले कदमों को '-' चिह्न से निरूपित किया जाता है। यदि मोहन शून्य के दाईं ओर 5 कदम चलता है, तो उसे +5 से निरुपत किया जा सकता है और यदि डेविड शून्य के बाईं ओर 5 कदम चलता है, तो उसे -5 से निरूपित किया सज सकता है। अब निम्नलिखित स्थानों को + या - चिह्न से निरूपित कीजिए :
शून्य के बाईं ओर 8 कदम
View Solutionनीचे दिए गए त्रिभुजों के कोणों और भुजाओं को क्रमशः चाँदे और रूलर से मापकर दी हुई सारणी में इनकी मापो को भरिए :
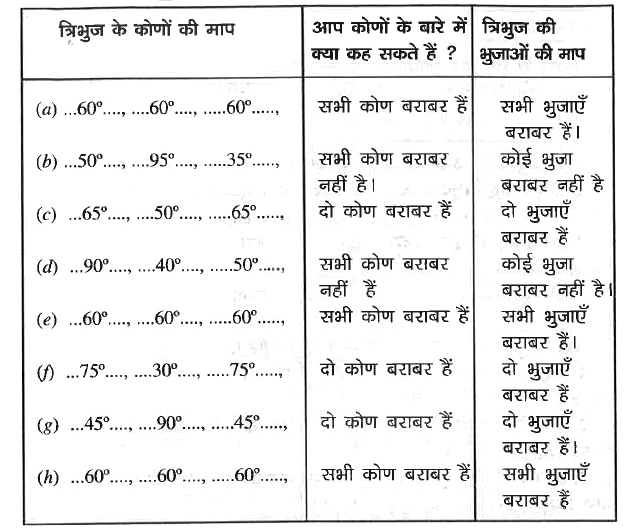
उपरोक्त कोण, त्रिभुज और उनकी भुजाओं की मापो को ध्यानपूर्वक देखिए । क्या इनके बारे में कोई बात कही जा सकती है ?
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionदिया है कि ¯a⋅¯b=0 और ¯aׯb=¯0. सदिश ¯a और ¯b के बारे में आप क्या निष्कर्ष निकाल सकते हैं ?
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionदर्शाइए कि दो शून्येतर सदिशों ¯a और ¯b के लिए,
|¯a|¯b+∣∣¯b∣∣¯a,|¯a|¯b−∣∣¯b∣∣¯a पर लम्ब है |
View Solution
