ABCD एक समांतर चतुर्भुज है और EF∣∣BD,EF का मध्यबिंदु R है तो साबित करे की BE=DF
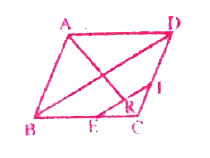
The correct Answer is:BE=DE
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - समांतर चतुर्भुजEXERCISE - EXERCISE-10.223videos
समांतर चतुर्भुज
- BOOK - KIRAN PUBLICATIONCHAPTER - वृत्त EXERCISE - अभ्यासार्थ प्रश्न18videos
वृत्त
- BOOK - KIRAN PUBLICATIONCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - Exercise - 11.132videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Similar Questions
रिक्त स्थानों को भरें।
किसी त्रिभुज PQR में PQ तथा PR के मध्य बिन्दु क्रमशः M और N है तो MN=….....01:37View Solution0.6 को pq के रूप में व्यक्त करें।
06:07View Solutionआधार BC के एक ही ओर बने ΔABC तथा ΔDBC में AD || BC है। यदि A ओर D से BC लम्ब डाले जाएँ तो उनकी लम्बाई में क्या संबंध होता है।
02:11View SolutionHow many lines of symmetry does the above figure have ?
01:31View SolutionWhich of the following are correct chain isomers of butane ? (i)
02:45View SolutionDetermine the point of symmetry of a regular hexagon.
02:17View SolutionDtermine the images of the following figure about the given line :
05:41View SolutionMatch the following Column A to Column B
 02:21View Solution
02:21View SolutionMatch the following Column A to Column B
 02:03View Solution
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionFind the area of the figure given below.
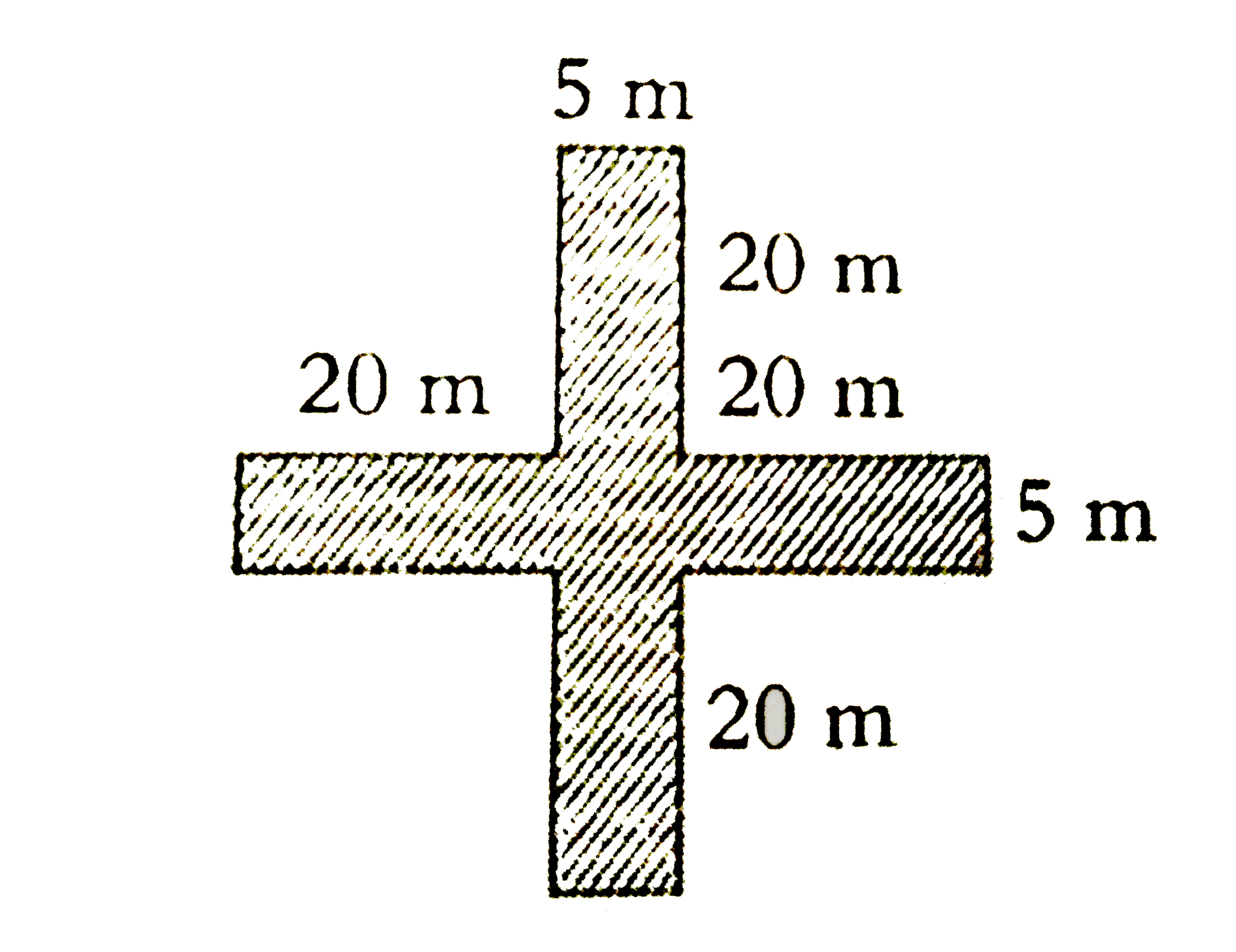 02:17View Solution
02:17View SolutionThe area of the shaded part in the figure given below is ______.
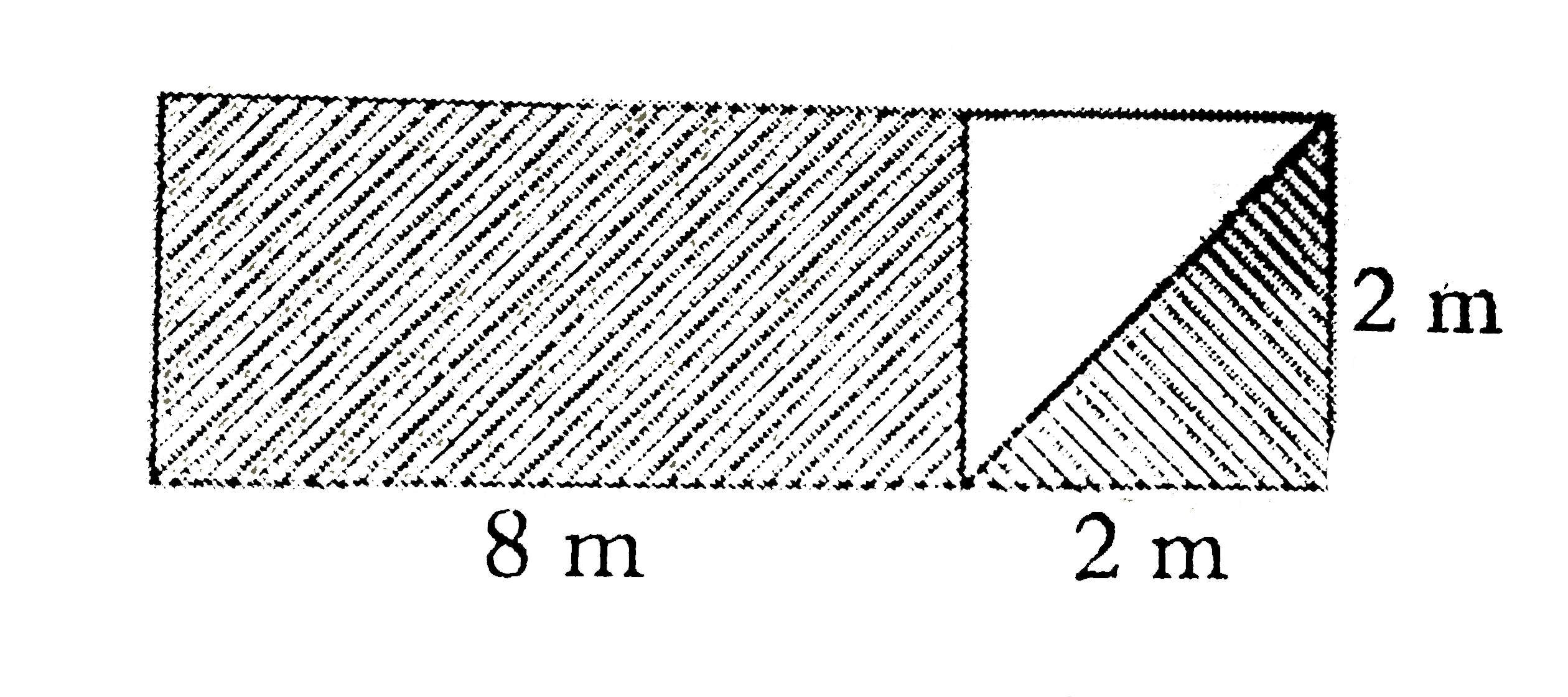 02:10View Solution
02:10View SolutionThe inequation represented by the graph given below is :
04:23View SolutionThe inequation that best describes the graph given below is _________
01:13View SolutionThe inequation that best describes the following graph is _________
02:24View SolutionWhich inequations represent the shaded region in the given figure
03:12View Solution

