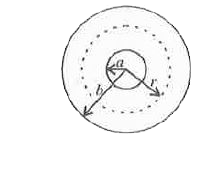
The figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density J=Cr2 where C is a constant. What is the magnitude of the magnetic field B at a point r, where a<r<b?
B=μ0πC4πr2(r2−a2)
B=μ0πC4πr2(r4−a4)
B=μ0πC4π(r2−a2)
B=μ0πC4π(r4−a4)
The correct Answer is:D
Given : Current density J=Cr2 For a region a<r<b.The Amperican loop is a circle labelled as 1 According to Ampere.s circuital law,
∮→B.d→l=μ0I
B(2πr)=μ0∫JdA=μ0∫raCr.2(2πr.dr.)
=μ0C2π∫r0r.3dr.=μ0C2π[r.44]ra
B2πr=μ0C2π4[r4−a4],B=μ0C4r[r4−a4]
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(FORCE ON A MOVING CHARGE IN UNIFORM ELECTRIC AND MAGNETIC FIELDS)
Explore 37 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(CYCLOTRON)
Explore 2 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(BIOT SAVART LAW AND ITS APPLICATIONS)
Explore 47 Videos
- ELECTROSTATICSBook:MTG GUIDEChapter:ELECTROSTATICSExercise:AIPMT/NEET (MCQ.s)
Explore 34 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
Similar Questions
The figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
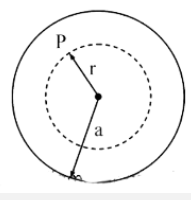
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :

View Solution
Knowledge Check
An infinitely long hollow conducting cylinder with inner radius r2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A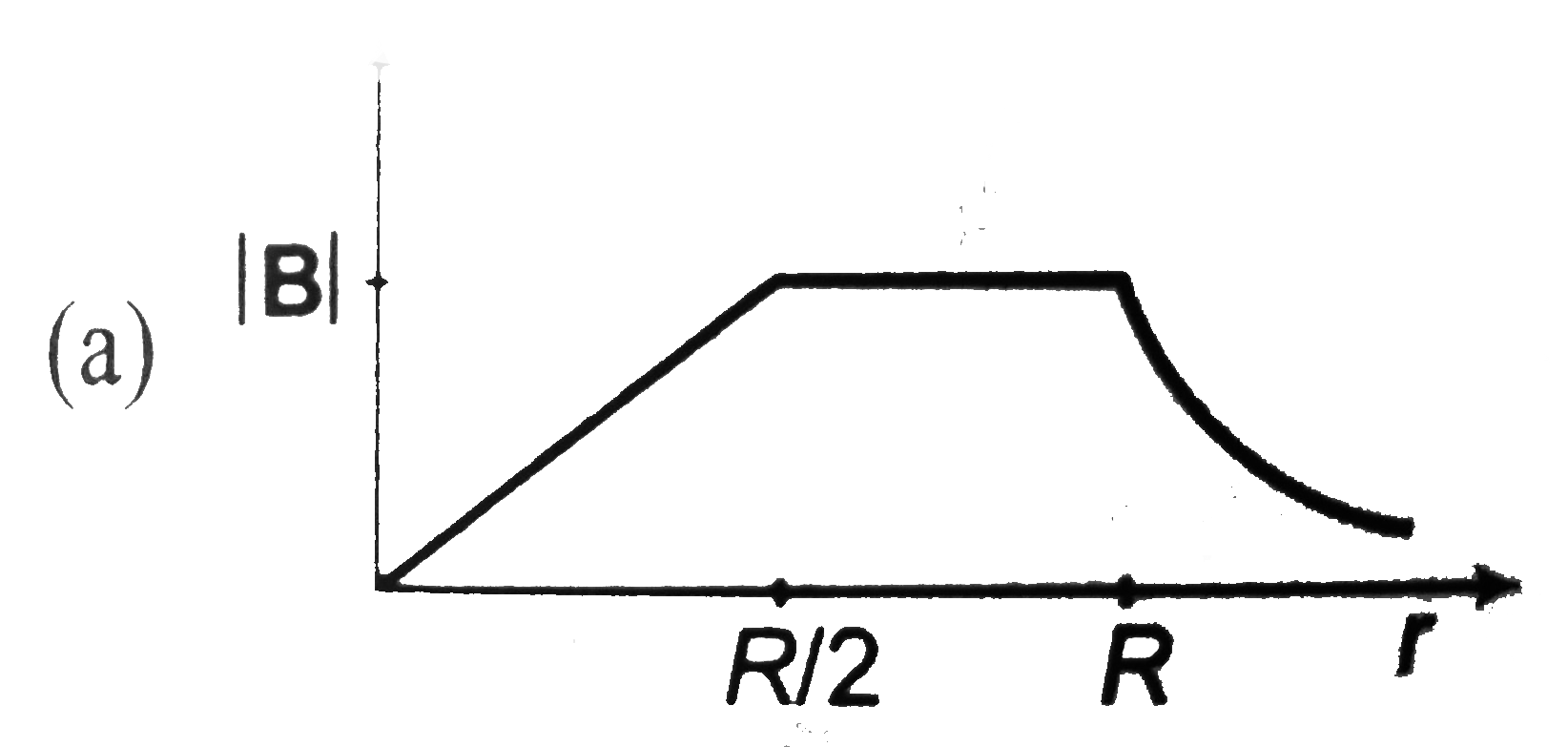 B
B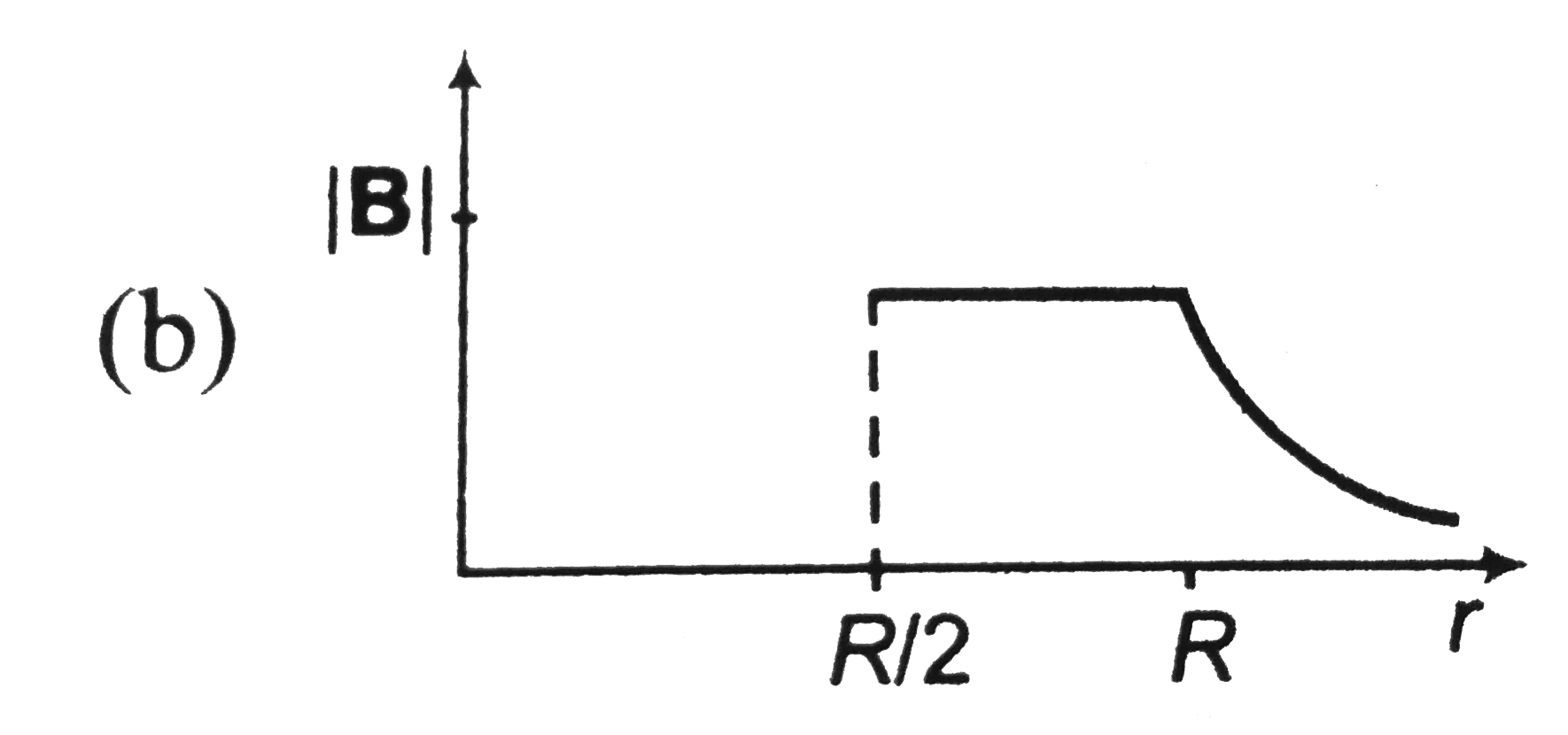 C
C D
D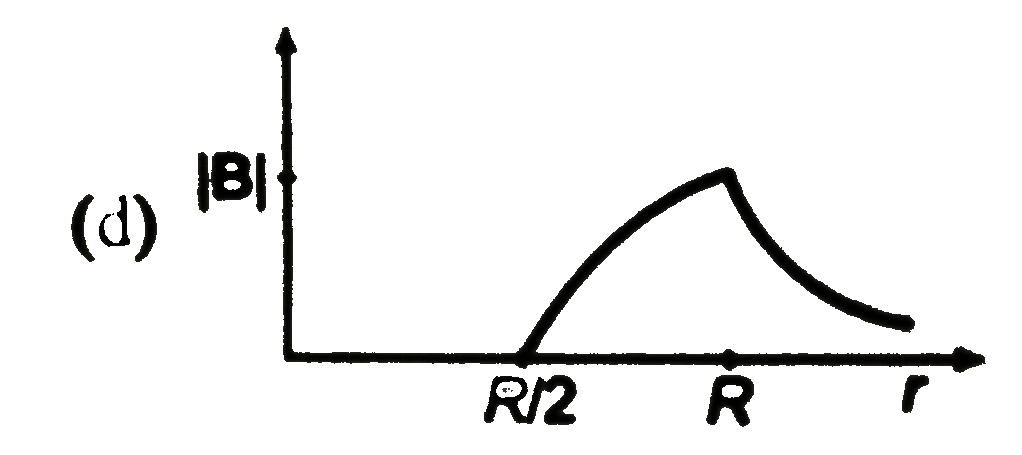
An infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A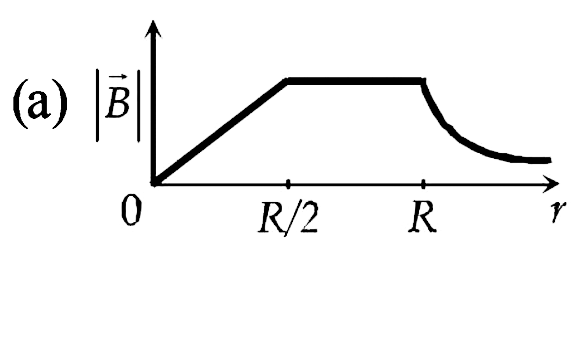 B
B C
C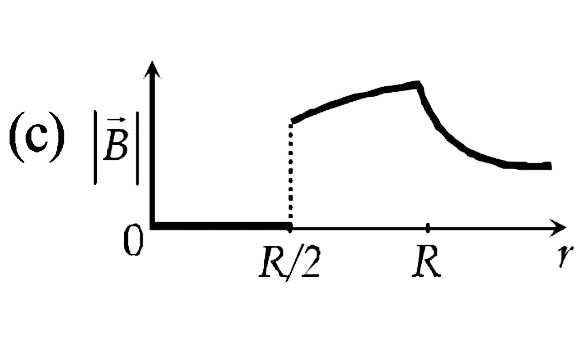 D
D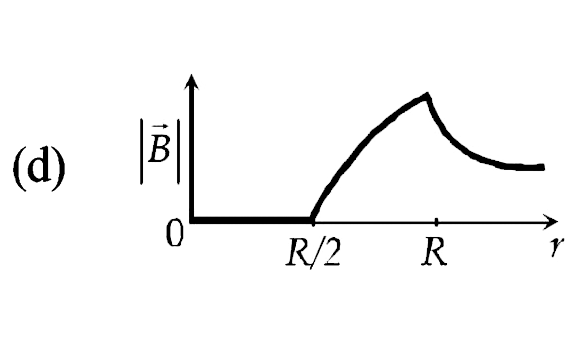
Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
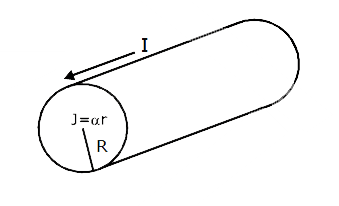 AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
An infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionA long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View SolutionA long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View Solution
