Can the altitude and median be same for a triangle?Solution in Punjabi
Step by step video & image solution for Can the altitude and median be same for a triangle? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
Similar Questions
Copy the figures with punched holes and find the axes of symmetry for the following:
09:09View SolutionIdentify the nets which can be used to make cubes (cut out copies of the nets and try it):
02:17View SolutionMedian divides a triangle into two triangles of the same area
43:20View SolutionCan the length of the median in a triangle to a side be less than the corresponding altitude?
View SolutionINTRODUCTION|MEDIANS AND ALTITUDES OF TRIANGLE|EXERCISE
04:10View SolutionCan the length of the median be equal to the altitude?
40:05View Solutionਚਿੱਤਰ ਬਣਾ ਕੇ ਪੜਤਾਲ ਕਰੋ ਕਿ ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਵਿੱਚ ਸਿਖ਼ਰ ਲੰਬ ਅਤੇ ਮੱਧਿਕਾ ਇਕ ਹੀ ਰੇਖਾਖੰਡ ਹੋ ਸਕਦਾ ਹੈ।
03:50View SolutionTriangle Properties||Isosceles triangle||Equilateral Triangle||ProOF OF Theorem 7.2 and 7.3||ProOF OF isosceles Triangle have Median,Angle bisector and altitude are same||Discussion OF Exercise 7.2 (Q.1 to Q.8)
03:58View SolutionA median and an altitude of an obtuse-angled triangle lie outside the triangle. It is true ?
03:45View SolutionIn a triangle ABC, AB = AC. Show that the altitude AD is median also.
07:41View SolutionIf in a triangle PQR;sinP,sinQ,sinR are in A.P; then (A)the altitudes are in AP (B)the altitudes are in HP (C)the altitudes are in GP (D)the medians are in AP
02:53View Solutionआकृति खींचकर पुष्टि कीजिये की एक समद्विबाहु त्रिभुज में शीर्षलम्ब त्रिभुज में शीर्षलम्ब व् मध्यिका एक ही रेखाखण्ड हो सकता हैं।
02:31View Solutionक्या किसी त्रिभुज की माध्यिका व शीर्षलंब एक ही रेखांखंड हो सकता है ?
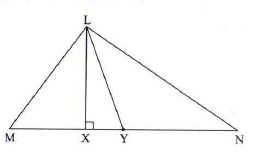
05:27View SolutionIn Δ LMN,…….. Is an altitude and ……. Is a median. (Write the names of appropriate segments)
 03:47View Solution
03:47View SolutionVerify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
View SolutionIf in a triangle PQR,sinP,sinQ,sinRare∈A.P. , then the altitudes are in A.P. the altitudes are in H.P. the medians are in G.P. the medians are in A.P.
01:19View Solution

