In fig.
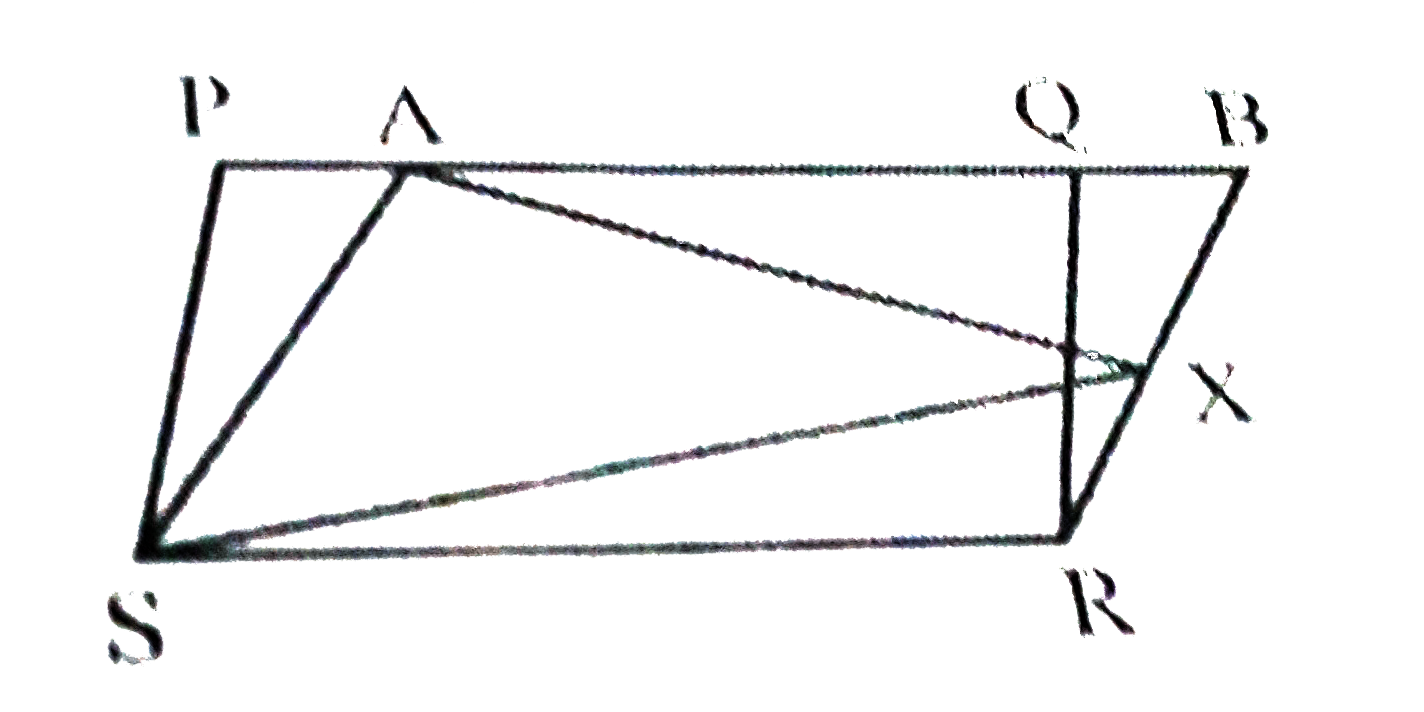
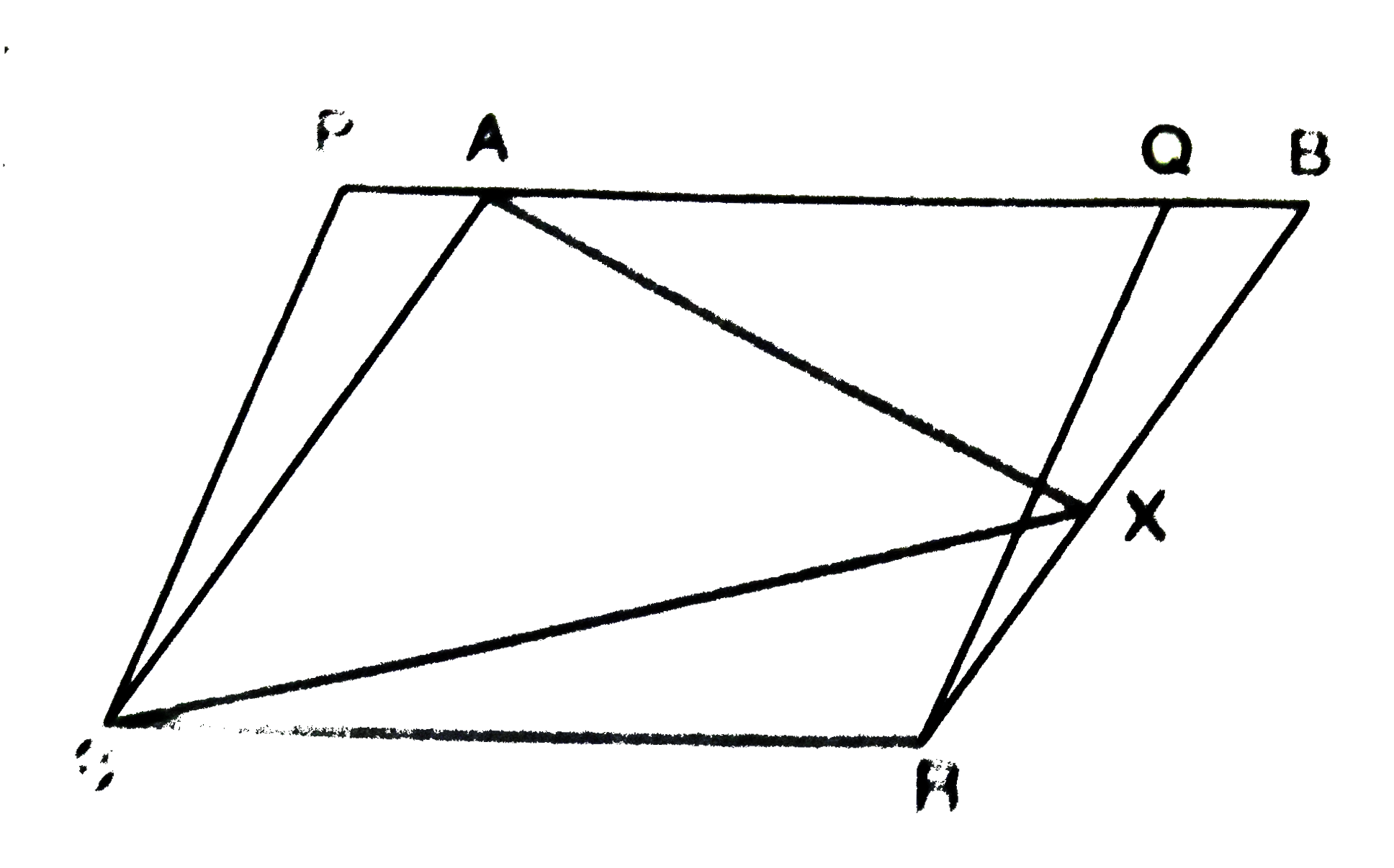
 PQRS and ABRS are parallelograms and X is any point on side BR. Show that ar(PQRS)=ar(ABRS).Solution in Punjabi
PQRS and ABRS are parallelograms and X is any point on side BR. Show that ar(PQRS)=ar(ABRS).Solution in Punjabi
Step by step video & image solution for In fig. PQRS and ABRS are parallelograms and X is any point on side BR. Show that ar(PQRS)=ar(ABRS). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
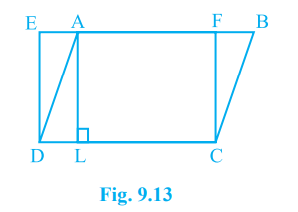
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
View SolutionGiven an arc of a circle, complete the circle.
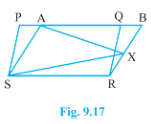
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View Solutionआकृति में, PQRS और ABRS समांतर चतुर्भुज है तथा X भुजा BR स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(PQRS)=ar(ABRS)
(ii) ar(AXS)=12ar(PQRS)
View Solutionचित्र में PQRS तथा ABRS समान्तर चतुर्भुज है तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाए कि
(i)ar(||gmPQRS)=ar(||gmABRS) (ii)ar(ΔAXS)=12ar(||gmPQRS)
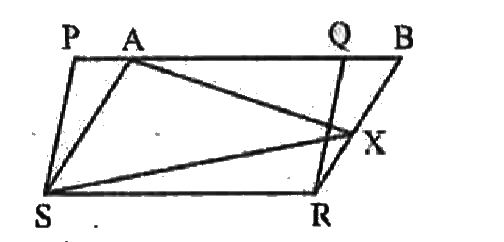
View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
View SolutionIN given figure, PQRS and ABRS are parallelograms and X is any point
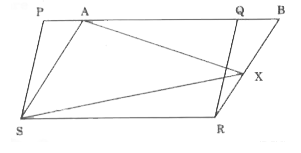
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS)
View Solutionआकृति में PQRS और ABRS समांतर चतुर्भज है तथा x भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
ar(AXS)=12ar(PQRS)
View SolutionPQRS and ABRS are two parallelograms. X is a point on the shoulder of BR (PQRS) y || = (ABRS) y ||
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View Solution
