Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (seeFig. 13.22). If each of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take ).
 Solution in Punjabi
Solution in Punjabi
Step by step video & image solution for Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (seeFig. 13.22). If each cm^3 of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take pi=22/7). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Rasheed got a playing lop (lattu ) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons.The top is shaped like a cone surmounted by a hemisphere (see Fig 13.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π=227)

View SolutionThe table below gives the percentage distribution of female teachers in the primary schools of rural areas of various states and union territories (U.T.) of India. Find the mean percentage of female teachers by all the three methods discussed in this section.

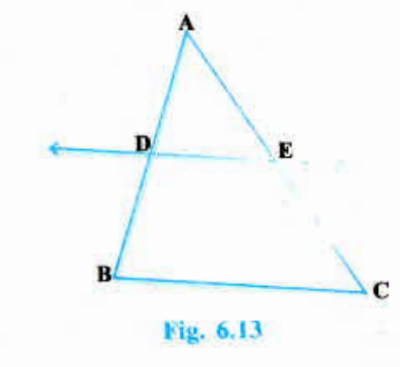
View Solutionif a line intersects sides AB and AC of a ΔABC at D and E respectively and is parallel to BC, prove that ADAB=AEAC (see Fig. 6,13).
View SolutionHanumappa and his wife Gangavva are busy making Jaggery out of sugar-cane. They have processed the sugar cane juice to make the molasses which is poured into moulds of the shape shown in the figure. It will be cooled to solidify in this shape to be sent to the market. Each mould is in the shape of a frustum of a cone having the diameters of its two circular ends as 30cm and 35cm and the height of the mould is 14cm. If each cm3 of molasses weighs about 1.2gm, find the weight of molasses that can be poured into each mould (Take π=22/7)
View SolutionHanumappa and his wife Gangavva are busy making Jaggery out of sugar-cane. They have processed the sugarcane juice to make the molasses which is poured into moulds of the shape shown in Fig 16.72. It will be cooled to solidify in this shape to be sent to the market. Each mould is in the sh ape of a frustum of a cone having the diameters of its two circular ends as 30 cm and 35 cm and the height of the mould is 14 cm. If each cm3 of molasses weighs about 1.2 gm, find the weight of molasses that can be poured into each mould (Take π=22/7 )
View SolutionA spherical cannonball 28 cm in diameter is melted and cast into a right circular cone mould, whose base is 35 cm in diameter. Find the height of the cone.
View Solutionहनुमप्पा और उसकी पत्नी गंगम्मा गन्ने के रस से गुड़ बना रहे है| उन्होंने गन्ने के रस को गर्म करके राब (शीरा) बना ली है, जिसे शंकु के छिन्नक के आकार के साँचों में डाला जाता है, जिनमे से प्रत्येक के दोनों वृत्तीय फलकों के व्यास क्रमशः 30 सेमी और 35 सेमी है तथा साँचे की ऊर्ध्वाधर ऊँचाई 14 सेमी है | यदि 1 घन सेमी राब का द्रव्यमान लगभग 1⋅2 ग्राम है तो प्रत्येक साँचे में भरी जा सकने वाली राब का द्रव्यमान ज्ञात करें |
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm, The diameters of its two circular ends are 16 cm and 12 cm. Find the capacity of the glass.
View SolutionA container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm, is completely filled with oil. If each cm3 of oil has mass 1.2 g then find the cost of oil in the container if it costs ₹40 per kg.
View SolutionIf the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm then its slant height is
View Solutionएक पात्र, एक शंकु के एक छिन्नक के आकार का है इसके दो वृत्तीय सिरों के व्यास 35 सेमी एवं 30 सेमी है तथा इसकी ऊर्ध्वाधर ऊँचाई 14 सेमी है । जो तेल से पूरा भरा है । यदि प्रत्येक सेमी3 तेल का द्रव्यमान 1.2 ग्राम है तब पात्र में तेल की लागत ज्ञात कीजिए यदि इसकी लागत रुपये 40/किग्रा है ।
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
View SolutionHanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (see Fig. 13.22). If each cm3 of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take π =227)
View SolutionA container in the shape of a frusum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm is completely filled with oil. If each cm3 of oil weighs 1.2g, find the cost of oil in the container at the rate Rs 40/kg.
View SolutionHanumappa and his wife Gangavva are busy making Jaggery out of sugar-cane. They have processed the sugarcane juice to make the molasses which is poured into moulds of the shape shown in Figure. It will be cooled to solidify in this shape to be sent to the market. Each mould is in the shape of a frustum of a cone having the diameters of its two circular ends as 30 cm and 35 cm and the height of the mould is 14 cm. If each cm3 of molasses weighs about 1.2 gm, find the weight of molasses that can be poured into each mould (Take π=22/7 )
View SolutionA spherical cannonball 28 cm in diameter is melted and cast into a right circular cone mould, whose base is 35 cm in diameter. Find the height of the cone.
View Solution
