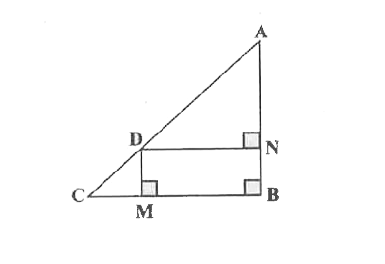
आकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD⊥AC तथा DM⊥BC और DN⊥AB है । सिद्ध कीजिए कि
(i) DM2=DN.MC (ii) DN2=DM.AN
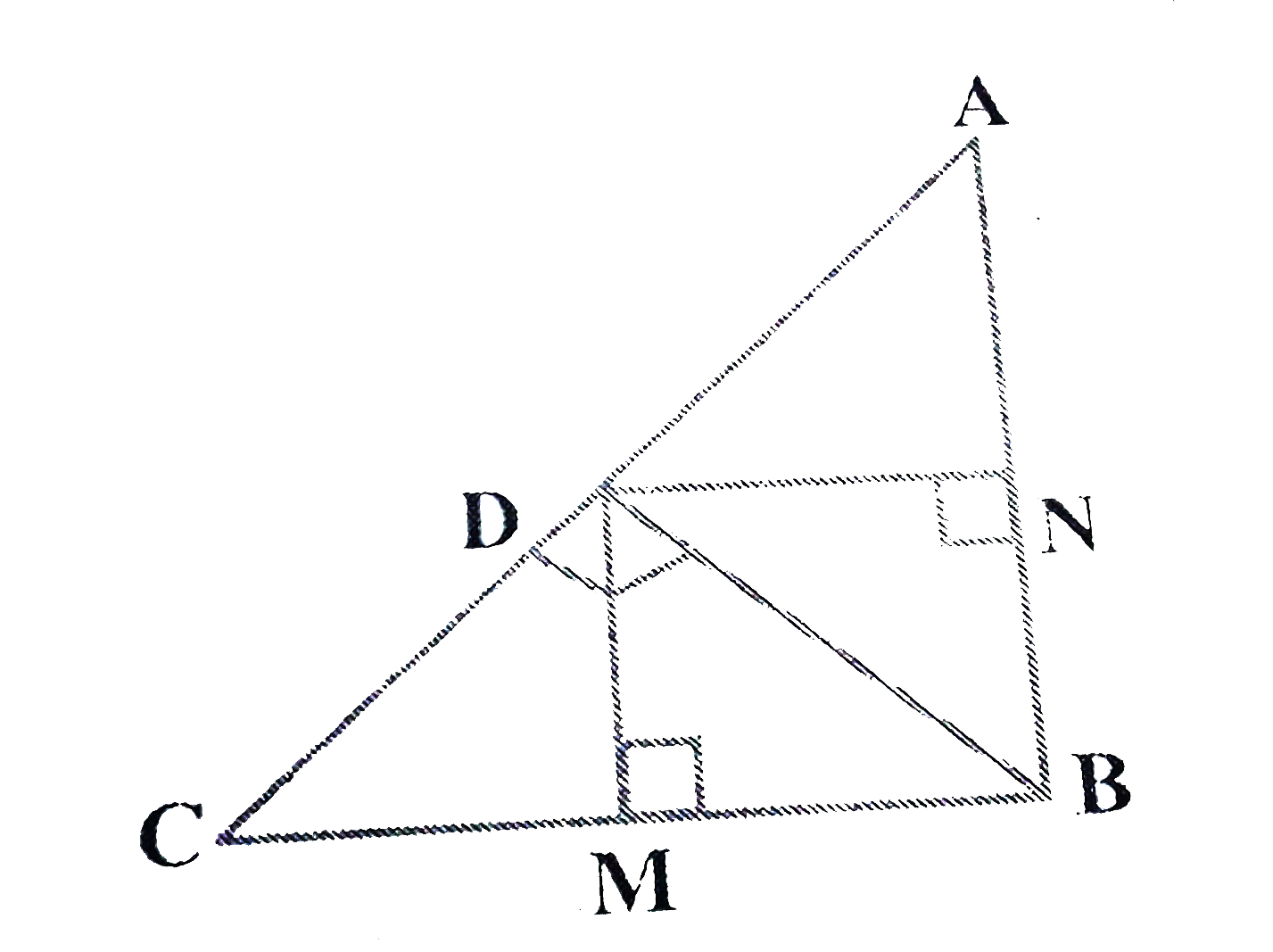
Step by step video & image solution for आकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD bot AC तथा DM bot BC और DN bot AB है । सिद्ध कीजिए कि (i) DM^(2)=DN.MC (ii) DN^(2)=DM.AN by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजBOOK - DEEPAK PUBLICATIONCHAPTER - त्रिभुजEXERCISE - बहुविकल्पीय-प्रश्न
58 Videos
- त्रिभुजBOOK - DEEPAK PUBLICATIONCHAPTER - त्रिभुजEXERCISE - परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न
21 Videos
- त्रिभुजBOOK - DEEPAK PUBLICATIONCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.5
20 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - DEEPAK PUBLICATIONCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - अभ्यास के लिए प्रश्न
14 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - DEEPAK PUBLICATIONCHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - अभ्यास के लिए प्रश्न
74 Videos
Similar Questions
यदि दो त्रिभुजों में संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसलिए ये समरूप होते हैं। सिद्ध करें।
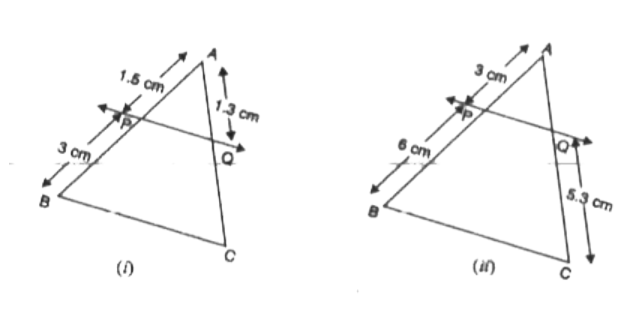
View Solutionयदि आकृति (1) और (i) में, PQ || BC हो, तो (i) में QC और (ii) में AQ ज्ञात कीजिए-
View Solutionयदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लंब डाला जाए तो इस लंब के दोनों ओर बने त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
View Solutionकिसी ऊर्ध्वाधर मीनार के पाद बिन्दु से 20 मीटर दूर धरती पर एक बिन्दु से मीनार के शिखर का उन्नयन कोण 60∘है | मीनार की ऊँचाई क्या है ?
View Solutionदो रेल पटरियां , समीकरणों x+2y−4=0 और 2x+4y−12=0 द्वारा निरूपित की गई है| इस स्थिति को ज्यामितीय रूप से व्यक्त कीजिए।
View SolutionMatch the following Column A to Column B

View Solutionआकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD⊥AC तथा DM⊥BC और DN⊥AB है । सिद्ध कीजिए कि
(i) DM2=DN.MC (ii) DN2=DM.AN

View Solutionआकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD⊥AC तथा DM⊥BC और DN⊥AB है । सिद्ध कीजिए कि
(i) DM2=DN.MC
(ii) DN2=DM.AN.

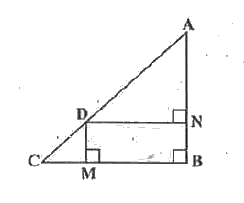
View SolutionIn Fig . D is a point on hypotenuse AC of ΔABC,⊥DM⊥BCandDN⊥AB. prove that :
DM2=DN.MC
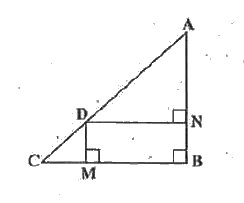
View SolutionIn Fig . D is a point on hypotenuse AC of ΔABC,⊥DM⊥BCandDN⊥AB. prove that :
DN2=DM.AN
View SolutionIn a △ABC, AB = AC and AD⊥BC, then BD = .......
View SolutionIn Fig. D is point on hypotenuse AC of ΔABC,BD⊥ACDM⊥BCandDN⊥AB . Prove that :
(i) DM2=DN.MC , (ii) DN2=DM.AN
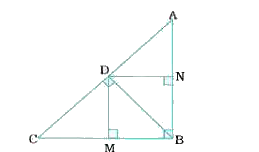
View SolutionABCD is a rectangle. AM bot BD And CN bot BD Then prove that BM^(2) + BN^(2) = DM^(2) + DN^(2)
View SolutionIn Fig. D is point on hypotenuse AC of ΔABC,BD⊥ACDM⊥BCandDN⊥AB . Prove that :
(i) DM2=DN.MC , (ii) DN2=DM.AN

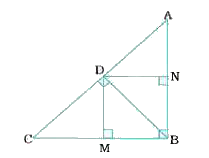
View SolutionIn the given figure, D is a point on hypotenuse AC of △ABC, such that BD⊥AC,DM⊥BC and DN⊥AB. Prove that :
DM2=DN⋅MC
View SolutionIn the given figure, D is a point on hypotenuse AC of △ABC, such that BD⊥AC,DM⊥BC and DN⊥AB. Prove that :
DN2=DM⋅AN
View Solution
