Two adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
The correct Answer is:117.58cm2
To find the area of the parallelogram with two adjacent sides measuring 10 cm and 12 cm, and one diagonal measuring 14 cm, we can follow these steps:
Step 1: Identify the sides and diagonal
Let the sides of the parallelogram be:
- Side A = 12 cm
- Side B = 10 cm
- Diagonal C = 14 cm
Step 2: Calculate the semi-perimeter (s) of triangle ABC
The semi-perimeter s is calculated using the formula:
s=A+B+C2
Substituting the values:
s=12+10+142=362=18 cm
Step 3: Apply Heron's formula to find the area of triangle ABC
Heron's formula for the area A of a triangle is given by:
A=√s(s−A)(s−B)(s−C)
Substituting the values:
A=√18(18−12)(18−10)(18−14)
Calculating each term:
- s−A=18−12=6
- s−B=18−10=8
- s−C=18−14=4
Now substituting these values into the formula:
A=√18×6×8×4
Step 4: Simplify the expression
Calculating the product:
18×6=108
108×8=864
864×4=3456
Thus, we have:
A=√3456
Step 5: Factor and simplify the square root
To simplify √3456:
3456=576×6
Since √576=24, we get:
A=24√6 cm2
Step 6: Calculate the area of the parallelogram
The area of the parallelogram is twice the area of triangle ABC:
Area of parallelogram=2×24√6=48√6 cm2
Final Answer
The area of the parallelogram is 48√6 cm2.
---
Let the sides of the parallelogram be:
- Side A = 12 cm
- Side B = 10 cm
- Diagonal C = 14 cm
The semi-perimeter s is calculated using the formula:
s=A+B+C2
Substituting the values:
s=12+10+142=362=18 cm
Heron's formula for the area A of a triangle is given by:
A=√s(s−A)(s−B)(s−C)
Substituting the values:
A=√18(18−12)(18−10)(18−14)
Calculating each term:
- s−A=18−12=6
- s−B=18−10=8
- s−C=18−14=4
A=√18×6×8×4
Calculating the product:
18×6=108
108×8=864
864×4=3456
Thus, we have:
A=√3456
To simplify √3456:
3456=576×6
Since √576=24, we get:
A=24√6 cm2
The area of the parallelogram is twice the area of triangle ABC:
Area of parallelogram=2×24√6=48√6 cm2
The area of the parallelogram is 48√6 cm2.
Topper's Solved these Questions
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12a
11 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
8 Videos
Similar Questions
The adjacent sides of a parallelogram are 21 cm and 28 cm. If its one diagonal is 35 cm, find the area of the parallelogram.
View SolutionTwo adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long, Find the area of the parallelogram. Also, find the distance between shorter sides.
View Solution
Knowledge Check
The adjacent sides of a parallelogram are in the ratio 5:3. if its perimeter is 96cm, find the sides of the parallelogram.
A30cm and 18cm.B55cm and 18cm.C26cm and 10cm.D37cm and 28cm.
One side of a parallelogram is 10 cm. If its diagonals are 12 cm and 16 cm. Find the area of the parallelogram.
View SolutionTwo sides of a parallelgram are 12 cm and 8 cm. If one of the interior angles is 135∘, then find area of the parallelogram.
View SolutionThe adjacent sides of a parallelogram ABCD measures 34cm and 20cm and the diagonal AC=42cm Then find its area
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
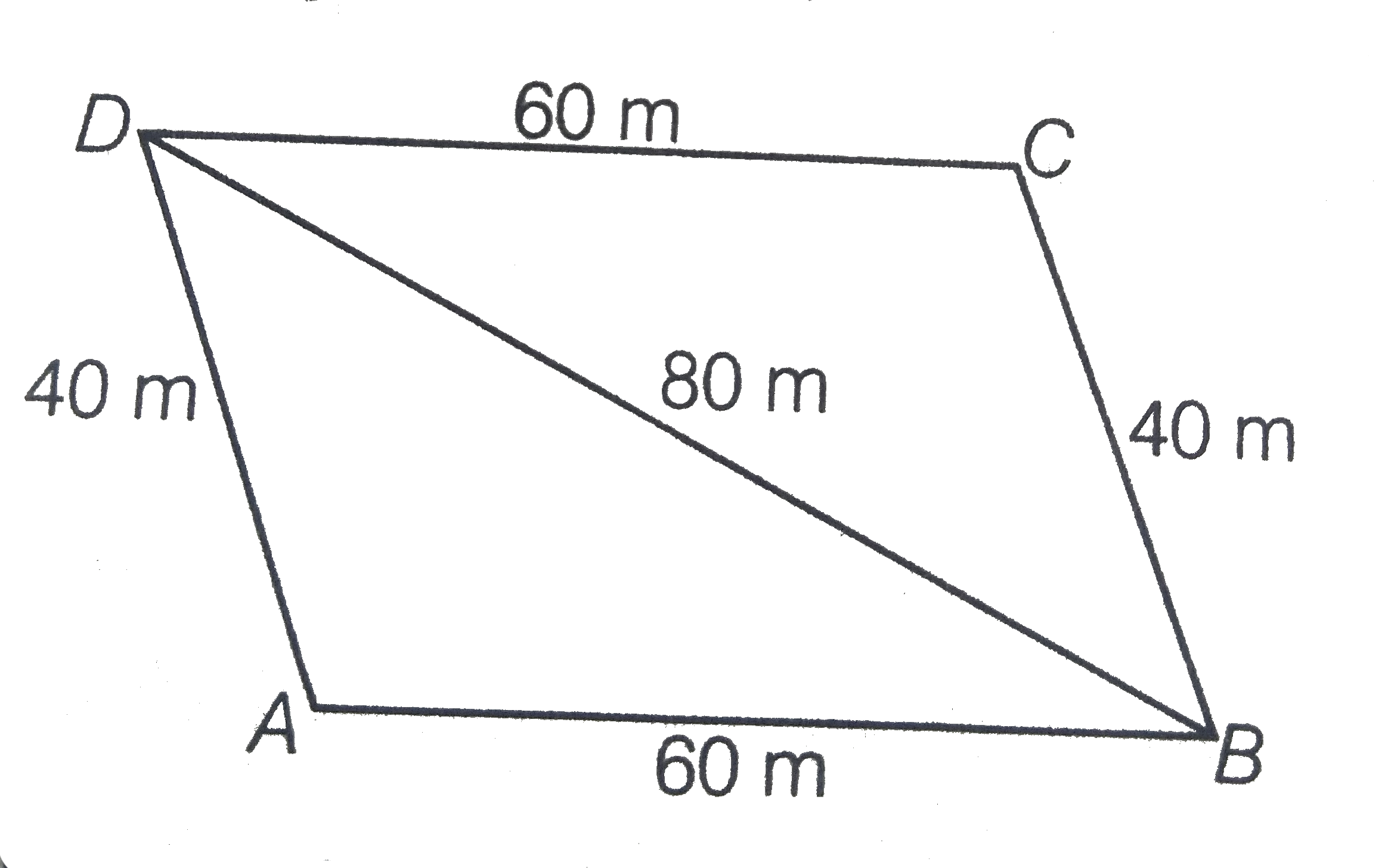
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
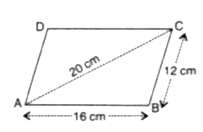
View SolutionOne side of a parallelogram is 20cm and its distance from the opposite side is 16cm. Find the area of the parallelogram.
View SolutionTwo adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between 15 cm sides is 8 cm, find the distance between 10 cm sides.
View Solution