If A⊆BandB⊂X, the the correct option is :
A⊂X
A⊆X
X⊂A
X⊆A
The correct Answer is:A
To solve the problem step by step, we will analyze the given conditions and determine the correct option based on the relationships between the sets A, B, and X.
1. Understanding the Given Information:
- We are given that A⊆B (A is a subset of B) and B⊆X (B is a subset of X).
- Additionally, it is stated that A=B.
2. Analyzing the First Condition:
- Since A⊆B and A=B, we can conclude that all elements of A are in B, and since A is equal to B, they contain the same elements. Therefore, A and B are identical sets.
3. Analyzing the Second Condition:
- The condition B⊆X means that all elements of B are also in X. Since we established that A=B, it follows that all elements of A are also in X.
4. Conclusion About Set A:
- From the above analysis, we can conclude that A⊆X is true because all elements of A are also in X.
5. Considering the Equality:
- Since A=B and B is not equal to X (as stated in the video), we cannot conclude that A=X. Therefore, while A is a subset of X, it is not equal to X.
6. Final Conclusion:
- The correct option is that A⊆X but A≠X.
Summary of the Answer:
- The correct option is that A⊆X and A≠X.
- We are given that A⊆B (A is a subset of B) and B⊆X (B is a subset of X).
- Additionally, it is stated that A=B.
- Since A⊆B and A=B, we can conclude that all elements of A are in B, and since A is equal to B, they contain the same elements. Therefore, A and B are identical sets.
- The condition B⊆X means that all elements of B are also in X. Since we established that A=B, it follows that all elements of A are also in X.
- From the above analysis, we can conclude that A⊆X is true because all elements of A are also in X.
- Since A=B and B is not equal to X (as stated in the video), we cannot conclude that A=X. Therefore, while A is a subset of X, it is not equal to X.
- The correct option is that A⊆X but A≠X.
- The correct option is that A⊆X and A≠X.
Topper's Solved these Questions
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1G
8 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1.1
6 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1E
15 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
Similar Questions
Knowledge Check
In the given representation of Calvin cycle, identify A, B and C and slect the correct option.
 AABC3PGARuBPTriose phosphateBABCRuBP3PGATriose phosphateCABCPEPQ∀Malic acidDABCPEPRuBPOAA
AABC3PGARuBPTriose phosphateBABCRuBP3PGATriose phosphateCABCPEPQ∀Malic acidDABCPEPRuBPOAA
Identify the figures A and B and select the correct option .

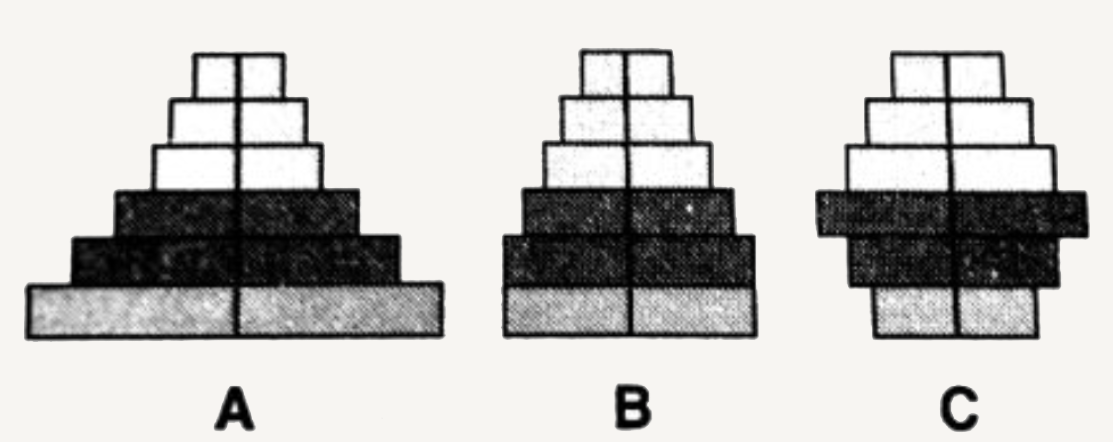
View SolutionRepresentation of age pyramids for the human population is given below. Identify A, B, and C by selecting the correct option .
View SolutionIf 25log5cosx=aandeln(−sinx)=b then the correct option is (where , a,b ∈ R) :-
View SolutionSelect the correct option for A, B,C & D
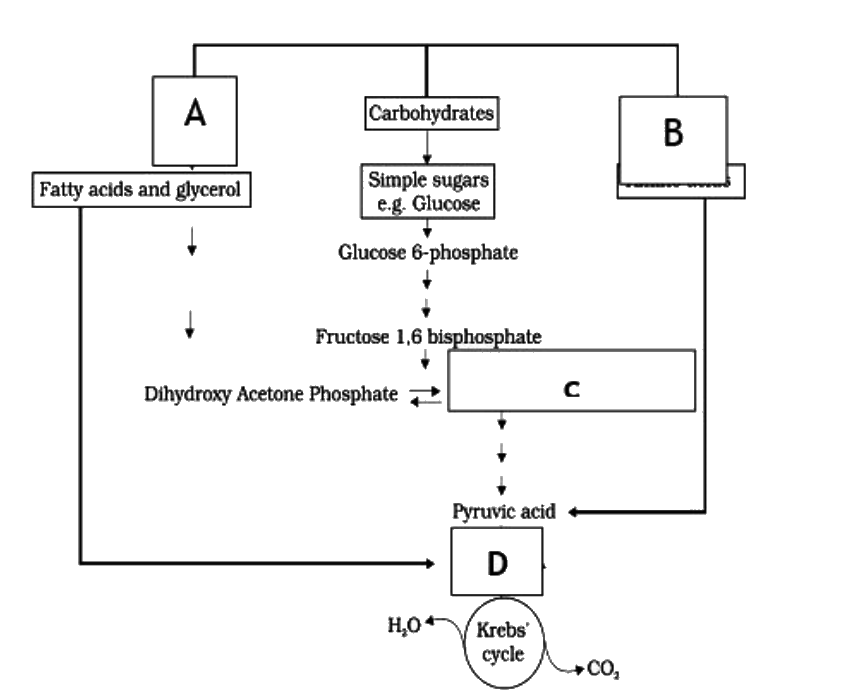
View SolutionRefer to the given figure.
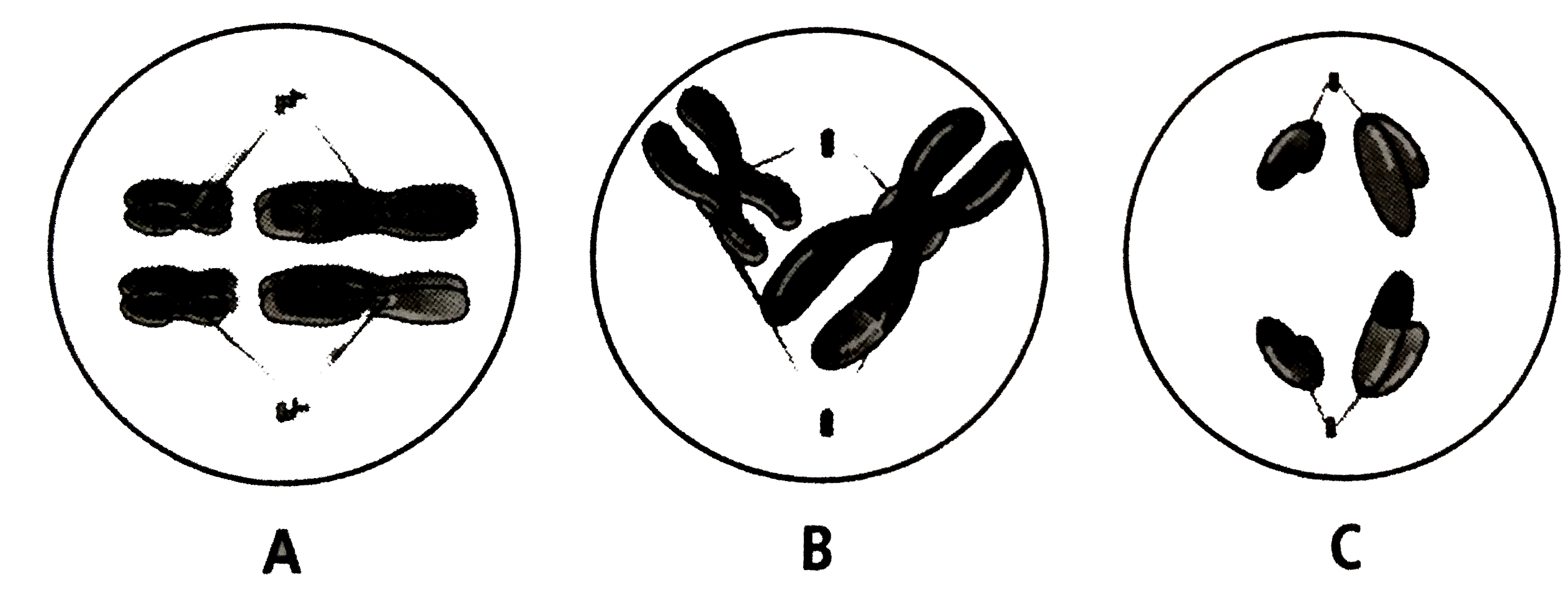
Identify A,B and C and select the correct option.
View SolutionIdentify the given figures A, B and C and select the correct option.

View SolutionIdentify the figures (A) and (B) and select the correct option.

View Solution
