The domain of f(x) = x2x2−3x+2 is :
R
R - {1}
R - {1,2}
R - {-1,-2}
The correct Answer is:c
To find the domain of the function f(x)=x2x2−3x+2, we need to determine the values of x for which the function is defined. The function is undefined when the denominator is equal to zero.
1. Identify the Denominator:
The denominator of the function is x2−3x+2.
2. Set the Denominator Equal to Zero:
To find the values of x that make the function undefined, we set the denominator equal to zero:
x2−3x+2=0
3. Factor the Quadratic Equation:
We can factor the quadratic expression:
x2−3x+2=(x−1)(x−2)
4. Find the Roots:
Setting each factor to zero gives us the roots:
x−1=0⇒x=1
x−2=0⇒x=2
5. Determine the Domain:
The function is undefined at x=1 and x=2. Therefore, the domain of f(x) includes all real numbers except these two values:
Domain of f(x)=R∖{1,2}
Final Answer:
The domain of f(x)=x2x2−3x+2 is all real numbers except 1 and 2.
---
The denominator of the function is x2−3x+2.
To find the values of x that make the function undefined, we set the denominator equal to zero:
x2−3x+2=0
We can factor the quadratic expression:
x2−3x+2=(x−1)(x−2)
Setting each factor to zero gives us the roots:
x−1=0⇒x=1
x−2=0⇒x=2
The function is undefined at x=1 and x=2. Therefore, the domain of f(x) includes all real numbers except these two values:
Domain of f(x)=R∖{1,2}
The domain of f(x)=x2x2−3x+2 is all real numbers except 1 and 2.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 2 G
10 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 2.1
10 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 2E
5 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
Similar Questions
Knowledge Check
The graph of f(x)=x−3x2−2x−3 is shown below. What is the domain of f(x) ?
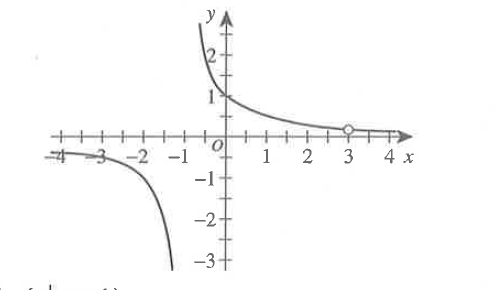 A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}
A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}
The domain of f(x)=log2(x+4)x2+3x+2 is
View SolutionFind the domain of f(x)=x2−9x−3
View SolutionThe domain of f(x)=log2(x+3)x2+3x+2, is
View SolutionFind the domain of f(x)=x2−4x−2
View SolutionFind the domain of f(x)=x2−36x+6
View SolutionThe domain of f(x)=log2(2x3−x2−4x+2), is
View SolutionThe domain of the function f(x)=x2−xx2+2x+1 is
View Solution
