The number of ways in which p+q things can be divided into two groups containing pandq things respectively is
(p+q+r)!p!q!r!
(pqr)!(p+q+r)!
(p+q+r)!(pqr)!
None of these
The correct Answer is:A
To find the number of ways in which p+q things can be divided into two groups containing p and q things respectively, we can follow these steps:
1. Understanding the Problem: We have a total of p+q items, and we need to divide them into two groups: one group containing p items and the other group containing q items.
2. Choosing Items for Group 1: We need to select p items from the total p+q items to form Group 1. The number of ways to choose p items from p+q items is given by the binomial coefficient:
(p+qp)
3. Understanding the Remaining Items: Once we have chosen p items for Group 1, the remaining q items will automatically go into Group 2. There is only one way to assign these remaining items to Group 2.
4. Using the Binomial Coefficient Formula: The binomial coefficient (nr) is calculated as:
(nr)=n!r!(n−r)!
Applying this to our case, we have:
(p+qp)=(p+q)!p!⋅q!
5. Final Result: Therefore, the total number of ways to divide p+q items into two groups of p and q items respectively is:
(p+q)!p!⋅q!
Final Answer:
The number of ways to divide p+q things into two groups containing p and q things respectively is:
(p+q)!p!⋅q!
(p+qp)
(nr)=n!r!(n−r)!
Applying this to our case, we have:
(p+qp)=(p+q)!p!⋅q!
(p+q)!p!⋅q!
The number of ways to divide p+q things into two groups containing p and q things respectively is:
(p+q)!p!⋅q!
Topper's Solved these Questions
- PERMUTATION AND COMBINATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Exercise I
10 Videos
- PERMUTATION AND COMBINATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Exercise 1
6 Videos
- PERMUTATION AND COMBINATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Exercise G
34 Videos
- MATHEMATICAL REASONING BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise
7 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise 4.1
1 Videos
Similar Questions
Knowledge Check
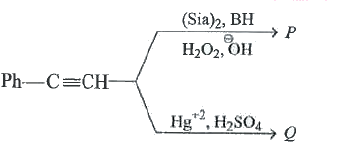
P and Q are respectively :A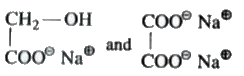 B
B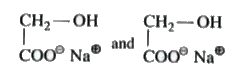 C
C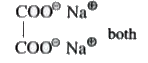 D
D
Number of ways in which 12 different things can be distributed in 3 groups, is
View Solution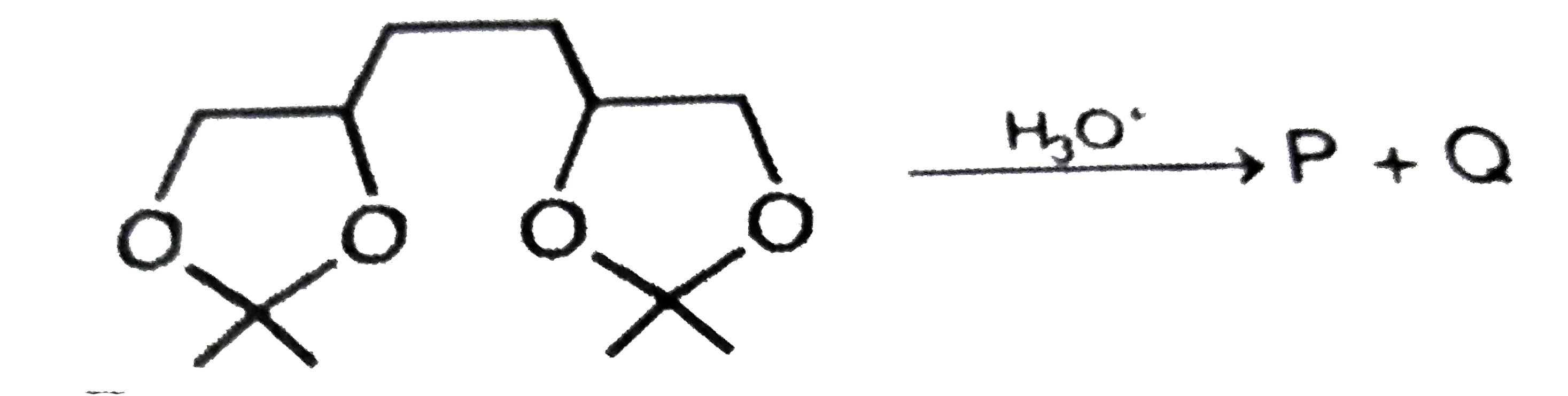
P and Q are respectively.
View SolutionNumber of ways in which 12 different things can be divided among five persons so that they can get 2,2,2,3,3 things respectively is
View Solution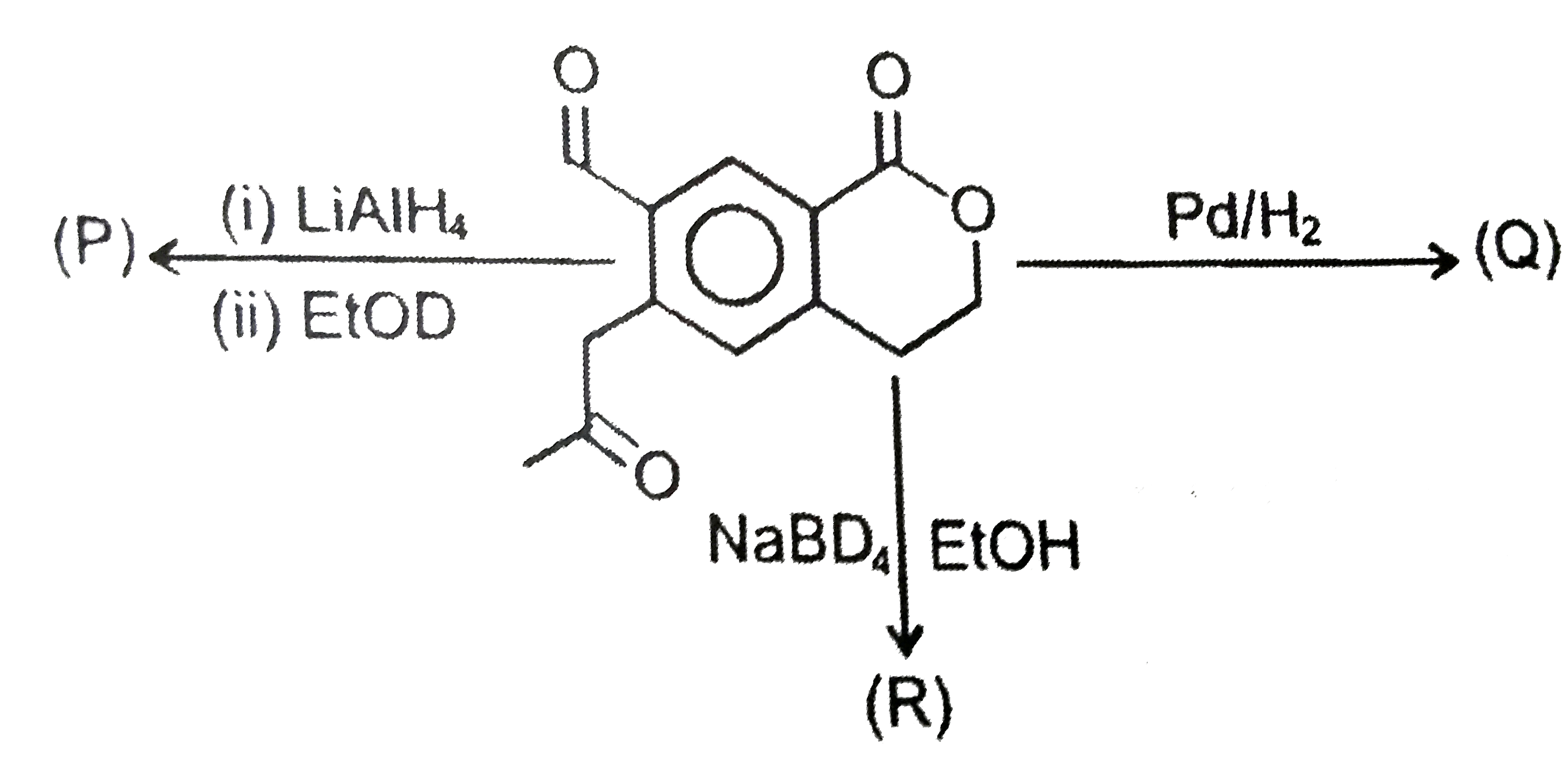
(P) and (Q) respectively are
View Solution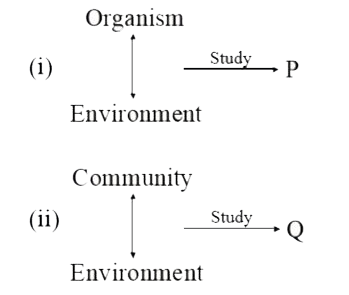
then P and Q are respectively called as.
View SolutionThe total number of ways of dividing mn things into n equal groups, is
View SolutionThe number of ways in which m+n(n≤m+1) different things can be arranged in a row such that no two of the n things may be together, is
View Solution
