Find the mean and variance for each of the data : First n natural numbers
To find the mean and variance of the first n natural numbers, we will follow these steps:
Step 1: Calculate the Mean
1. Sum of the first n natural numbers:
The formula for the sum of the first n natural numbers is given by:
Sn=n(n+1)2
2. Mean (x̄):
The mean is calculated by dividing the sum by the number of terms (n):
Mean=Snn=n(n+1)2n=n+12
Step 2: Calculate the Variance
1. Sum of the squares of the first n natural numbers:
The formula for the sum of the squares of the first n natural numbers is:
Sn2=n(n+1)(2n+1)6
2. Variance (σ²):
The variance is calculated using the formula:
σ2=Sn2n−(Snn)2
Substituting the values:
σ2=n(n+1)(2n+1)6n−(n+12)2
Simplifying this:
σ2=(n+1)(2n+1)6−(n+1)24
3. Finding a common denominator:
The common denominator for 6 and 4 is 12. Thus, we rewrite the terms:
σ2=2(n+1)(2n+1)12−3(n+1)212
4. Combine the fractions:
σ2=2(n+1)(2n+1)−3(n+1)212
5. Simplifying the numerator:
Expanding and simplifying:
σ2=(n+1)(4n+2−3n−3)12=(n+1)(n−1)12
Final Results
- Mean:
Mean=n+12
- Variance:
σ2=(n2−1)12
The formula for the sum of the first n natural numbers is given by:
Sn=n(n+1)2
The mean is calculated by dividing the sum by the number of terms (n):
Mean=Snn=n(n+1)2n=n+12
The formula for the sum of the squares of the first n natural numbers is:
Sn2=n(n+1)(2n+1)6
The variance is calculated using the formula:
σ2=Sn2n−(Snn)2
Substituting the values:
σ2=n(n+1)(2n+1)6n−(n+12)2
Simplifying this:
σ2=(n+1)(2n+1)6−(n+1)24
The common denominator for 6 and 4 is 12. Thus, we rewrite the terms:
σ2=2(n+1)(2n+1)12−3(n+1)212
σ2=2(n+1)(2n+1)−3(n+1)212
Expanding and simplifying:
σ2=(n+1)(4n+2−3n−3)12=(n+1)(n−1)12
Mean=n+12
σ2=(n2−1)12
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE20videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
Similar Questions
Find the mean and variance for each of the data in Question:
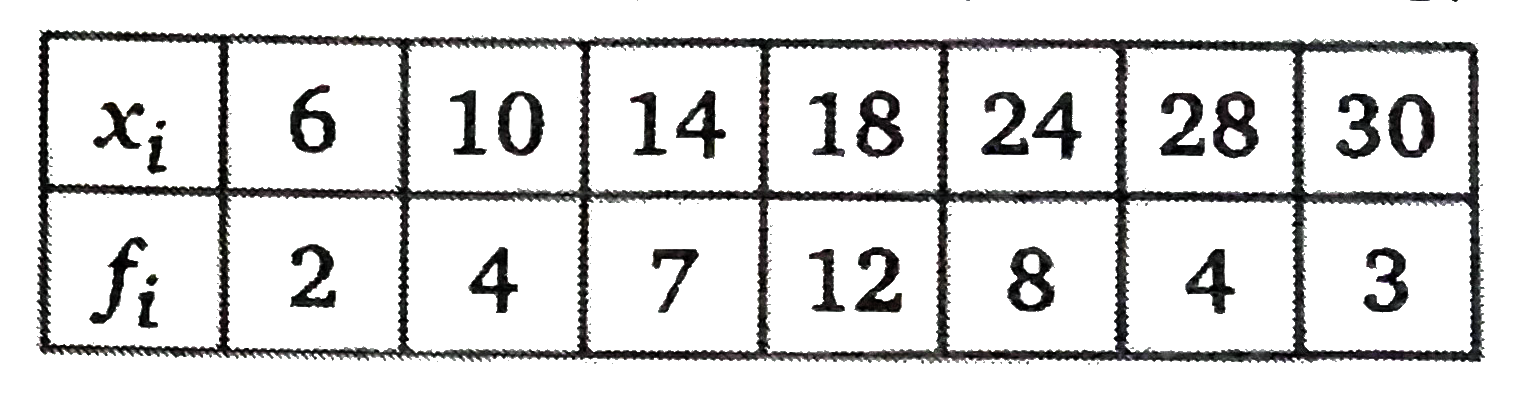 View Solution
View SolutionFind the mean and variance for each of the data in Question:
 View Solution
View SolutionFind the mean and variance for each of the data : First 10 multiples of 3.
View SolutionThe S.D. of the first n natural numbers is
View SolutionFind the sum of first n natural numbers.
View SolutionFind the sum of first n natural numbers.
View SolutionFind the sum of first n natural numbers.
View SolutionThe variance of first n natural number is:
View SolutionCalculate the mean deviation about the mean of the set of first n natural numbers when n is odd natural number.
View SolutionCalculate the mean deviation about the mean of the set of first n natural numbers when n is even natural number.
View Solution

