P is any point in the angle ABC such that the perpendicular drawn from P on AB and BC are equal. Prove that BP bisects angle ABC.
Step by step video & image solution for P is any point in the angle ABC such that the perpendicular drawn from P on AB and BC are equal. Prove that BP bisects angle ABC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (long Answer Type Question)
8 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Triangle ABC is isosceles with AB=ACandBC=65cm. P is a point on BC such that the perpendiculardistances from P to ABandAC are 24cmand36cm, respectively. The area of triangle ABC (in sq cm is)
View SolutionIf AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
View SolutionThe vertices of a triangle ABC are the points (0,b),(−a,0),(a,0). Find the locus of a point P which moves inside the triangle such that the product of perpendiculars from P to ABandAC is equal to the square of the perpendicular to BC.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
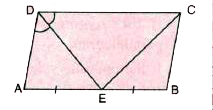
CE bisects angle C
View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View SolutionBD is the disector of angle ABC. From a point P in BD, perpendiculars PE and PF are drawn to AB and BC respectively, prove that :
(i) Triangle BEP is conguent to triangle BFP (ii) PE=PF.
View SolutionA triangle ABC has ∠B=∠C. Prove that :
(i) the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) the perpendicular from B and C to the opposite sides are equal.
View SolutionABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) 1p2=1a2+1b2
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View Solution
