Construct an equilateral triangle whose side is 5 cm.
Step-by-Step Solution to Construct an Equilateral Triangle with Side 5 cm
Step 1: Draw a Base Line Segment
- Using a ruler, draw a straight line segment of length 5 cm. Label the endpoints as points B and C.
Hint: Use a ruler to measure exactly 5 cm for accuracy.
---
Step 2: Set the Compass Width
- Take a compass and adjust its width to 5 cm. This is the length of the sides of the equilateral triangle.
Hint: Ensure the compass is not too loose; it should hold the 5 cm measurement firmly.
---
Step 3: Draw Arcs from Point B
- Place the pointed end of the compass on point B and draw an arc above the line segment BC.
Hint: Make sure to draw the arc wide enough to intersect with the arc from point C later.
---
Step 4: Draw Arcs from Point C
- Now, place the pointed end of the compass on point C and draw another arc that intersects the first arc drawn from point B.
Hint: The intersection of the two arcs will help you find the third vertex of the triangle.
---
Step 5: Mark the Intersection Point
- Label the intersection point of the two arcs as point A.
Hint: This point A is crucial as it will be the third vertex of your equilateral triangle.
---
Step 6: Connect the Points
- Use a ruler to draw straight lines connecting points A to B and A to C.
Hint: Ensure the lines are straight and clearly defined to represent the sides of the triangle.
---
Step 7: Label the Triangle
- Finally, label the triangle as ABC, and indicate that each side is 5 cm.
Hint: Clearly labeling your triangle helps in understanding and presenting your construction.
---
Final Note:
You have successfully constructed an equilateral triangle ABC where each side measures 5 cm.
- Using a ruler, draw a straight line segment of length 5 cm. Label the endpoints as points B and C.
- Take a compass and adjust its width to 5 cm. This is the length of the sides of the equilateral triangle.
- Place the pointed end of the compass on point B and draw an arc above the line segment BC.
- Now, place the pointed end of the compass on point C and draw another arc that intersects the first arc drawn from point B.
- Label the intersection point of the two arcs as point A.
- Use a ruler to draw straight lines connecting points A to B and A to C.
- Finally, label the triangle as ABC, and indicate that each side is 5 cm.
You have successfully constructed an equilateral triangle ABC where each side measures 5 cm.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
Similar Questions
Construct an equilateral triangle whose altitude is 4 cm.
View SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionConstruct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
View SolutionConstruct on equilateral triangle each of whose sides is of length 4.6cm.
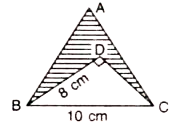
View SolutionThe given figure shows an equilateral triangle ABC whose side is 10 cm and a right-angled BDC inside it, whose side BD = 8 cm and ∠D=90∘. Find the area of the shaded portion.

View SolutionFind the area of an equilateral triangle whose side is a cm.
View SolutionFind the area of an equilateral triangle, whose one side is a cm.
View SolutionWhat is the area of an equilateral triangle whose sides measure 8 cm long?
View SolutionThe given figure shows an equilateral triangle ABC whose each side is 10 cm and a right-angled triangle BDC whose side BD = 8 cm and ∠D=90∘. Find the area of the shaded portion.
View SolutionCalculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
View Solution
