If the points A(1,3), B(−2,1), C(x,2) and D(−1,5) are given and AB is perpendicular to CD, find the value of x.
To solve the problem step by step, we need to find the value of x such that the line segment AB is perpendicular to the line segment CD.
Step 1: Identify the coordinates of the points
The points given are:
- A(1,3)
- B(−2,1)
- C(x,2)
- D(−1,5)
Step 2: Calculate the slope of line segment AB
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
For points A(1,3) and B(−2,1):
- x1=1,y1=3
- x2=−2,y2=1
Now, substituting these values into the slope formula:
mAB=1−3−2−1=−2−3=23
Step 3: Calculate the slope of line segment CD
Using the same slope formula for points C(x,2) and D(−1,5):
- x1=x,y1=2
- x2=−1,y2=5
Substituting these values:
mCD=5−2−1−x=3−1−x
Step 4: Set up the equation for perpendicular lines
Since AB is perpendicular to CD, the product of their slopes must equal −1:
mAB⋅mCD=−1
Substituting the slopes we found:
(23)⋅(3−1−x)=−1
Step 5: Solve for x
Now, simplifying the equation:
2⋅33⋅(−1−x)=−1
This simplifies to:
2−1−x=−1
Cross-multiplying gives:
2=−1(−1−x)
2=1+x
Subtracting 1 from both sides:
x=2−1=1
Final Answer
Thus, the value of x is:
1
The points given are:
- A(1,3)
- B(−2,1)
- C(x,2)
- D(−1,5)
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
For points A(1,3) and B(−2,1):
- x1=1,y1=3
- x2=−2,y2=1
mAB=1−3−2−1=−2−3=23
Using the same slope formula for points C(x,2) and D(−1,5):
- x1=x,y1=2
- x2=−1,y2=5
mCD=5−2−1−x=3−1−x
Since AB is perpendicular to CD, the product of their slopes must equal −1:
mAB⋅mCD=−1
Substituting the slopes we found:
(23)⋅(3−1−x)=−1
Now, simplifying the equation:
2⋅33⋅(−1−x)=−1
This simplifies to:
2−1−x=−1
Cross-multiplying gives:
2=−1(−1−x)
2=1+x
Subtracting 1 from both sides:
x=2−1=1
Thus, the value of x is:
1
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
Similar Questions
Knowledge Check
In the given figure, AB∣∣CD. Find the value of x
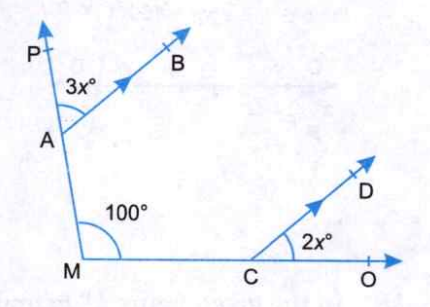 A20B25C40D60
A20B25C40D60
Using vectors show that the points A(-2,3,5), B(7,0,-1), C(-3,-2,-5) and D(3,4,7) are such that AB and CD intersect at the point P(1,2,3).
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
equation of the perpendicular bisector of AB.
View SolutionThe line joining the points A(2,1), and B(3,2) is perpendicular to the line (a2)x+(a+2)y+2=0. Find the values of a.
View SolutionIf A (6,-6,0), B(-1,-7,6), C (3,-4, 4) and D (2,-9,2) be four points in space. Show that AB is perpendicular to CD.
View SolutionFour points A(6, 3), B(−3, 5), C(4, −2) and D(x, 3x) are given in such a way that DBCABC=12 , find x .
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
slope of perpendicular to AB
View SolutionShow that the points A(6,−7,0),B(16,−19,−4),C(0,3,−6) and D(2,−5,10) are such that ABandCD intersect at the point P(1,−1,2).
View Solution
