Question

If the mid-point of the line segment between the axes of a line is $(p,q)$ then find the equation of the line.

Explanation

Let the equation of the line be
`(x)/(a)+(y)/(b)=1`…..`(1)`

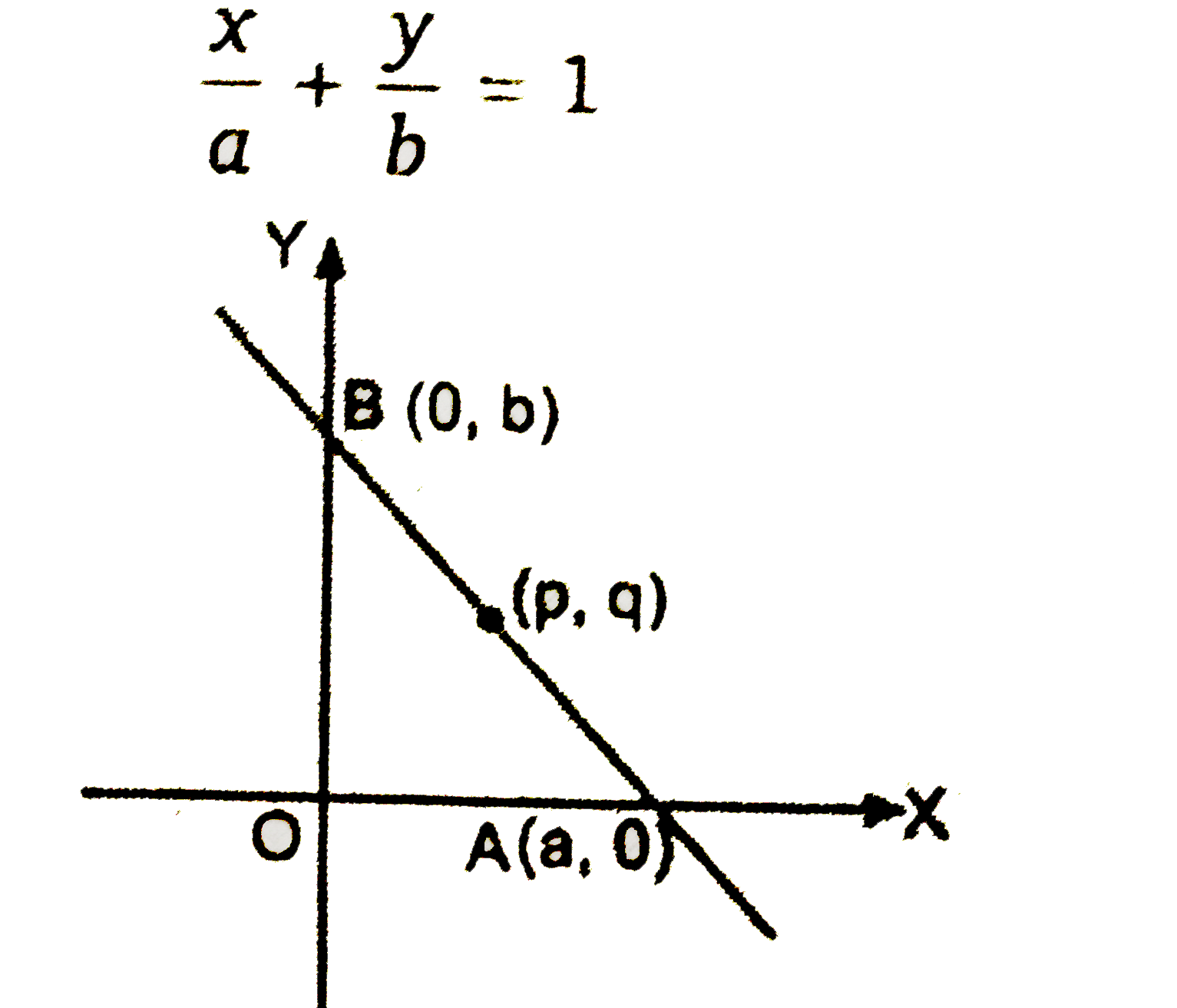
This line meets `X`-axis at point `A(a,0)` and `Y`-axis at point `B(0,b)`.
Now, the mid-point of line-segment `AB` is `(p,q)`
`:. (a+0)/(2)=p` and `(0+b)/(2)=q`
`implies a=2p` and `b=2q`
From eq. `(1)`, the equation of straight line is
`(x)/(2p)+(y)/(2q)=1`
`implies (x)/(p)+(y)/(q)=2`