Find the co-ordinates of the foot of perpendicular drawn from the point (3,−3) to the line x−2y=4.
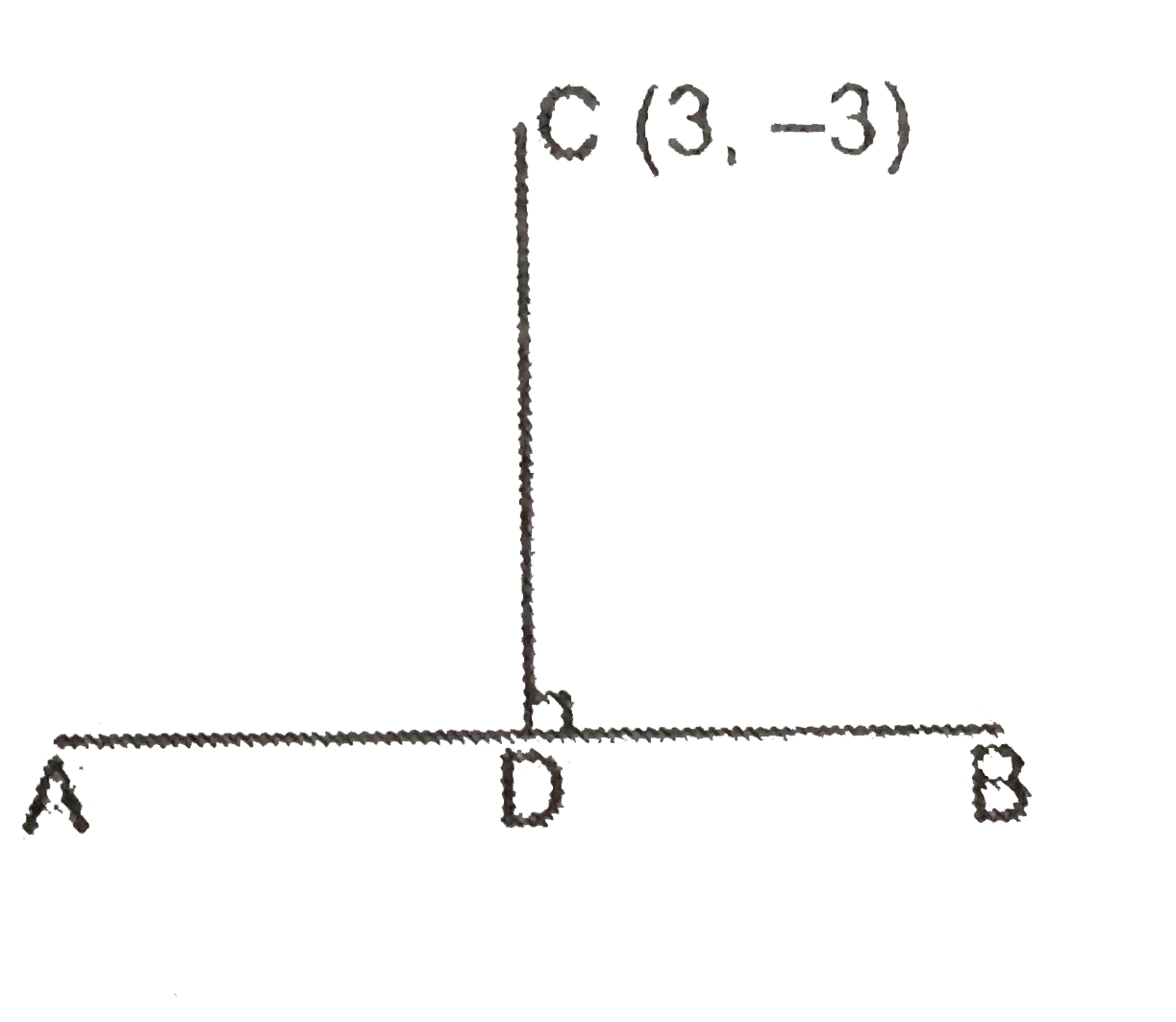
Let the line x−2y=4 be AB and CD is perpendicular from point C(3,−3)AB.
Now, for the slope of AB
2y=x−4
⇒y=12x−2
∴ Slope of AB
m1=12
Slope of perpendicular line CD
m2=−1m1=−2
Equation of CD
(−y−3)=−2(x−3)
⇒y+3=−2x+6
⇒2x+y=3
On solving the equation of CD and equation of AB, x=2, y=−1
∴ Co-ordinates of foot of perpendicular D=(2,−1)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the coordinates of the foot of the perpendicular drawn from the point (2,3) to the line y=3x+4
View SolutionFind the coordinates of the foot of perpendicular from the point (−1,3) to the line 3x−4y−16=0.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (1,−2) on the line y=2x+1.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (1,−2) on the line y=2x+1.
View SolutionFind the co-ordiantes of the foot of perpendicular drawn from the point (1,2,3) to the line x−63=y−72=z−7−2.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point P(1,-2) on the line y = 2x +1. Also, find the image of P in the line.
View SolutionFind the coordinates of the foot o the perpendicular from the point (-1, 3) to the line 3x−4y−16=0
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (5, 4,2) to the line x+12=y−33=z−1−1 . Hence or otherwise deduce the length of the perpendicular.
View SolutionFind the co-ordinates of the foot of perpendicular drawn from point A(1,6,3) to the line x1=y−12=z−23.
View SolutionFind the coordinates of the foot of perpendicular from the point (−1,3)to the line 3x−4y−16=0.
View Solution

