A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:n. Find the equation of the line.
Slope of a line joining the points (1,0) and (2,3) is
m1=3−02−1=3
If the slope of perpendicular line is m2 then
m1m2=−1
⇒m2=−13
Coordinates of the point dividing the line segment joining the points (1,0) and (2,3) in the ratio 1:n are
=(1×2+n×11+n,1×3+n×01+n)=(n+2n+1,3n+1)
Now, equation of line
y−3n+1=−13(x−n+2n+1)
⇒3(n+1)y−9=−(n+1)x+(n+2)
⇒(n+1)x+3(n+1)y=(n+11)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
A line perpendicular to the in segment joining the points (1,0) and (2,3) divides it in the ratio 1:n . Find the equation of the line.
View SolutionIn which ratio the line segment joining the points (3, 0, 5) and (-2, 3, 2) is divided by YZ-plane?
View SolutionFind the equation of perpendicular bisector of line segment joining the points (1,5) and (3,−1)
View SolutionFind the ratio in which the line segment joining of the points (1,2) and (−2,3) is divided by the line 3x+4y=7
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,1) and (2,3).
View SolutionXY plane divides the line segment joining the points (1,2,-3) and (0,1,5) in the ratio __________
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,0) and (3,5).
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
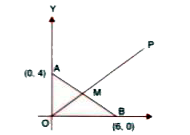
length of BPView SolutionFind the ratio in which the line segment joining the points (–3,10) and (6,–8) is divided by (–1,6).
View SolutionThe point which divides the line segment joining the points (8,–9) and (2,3) in ratio 1 : 2 internally lies in the
View Solution

