The hypotenuse of a right angled triangle has its ends at the points (1, 3) and ( −4, 1) . Find the equation of the legs (perpendicular sides) of the triangle.
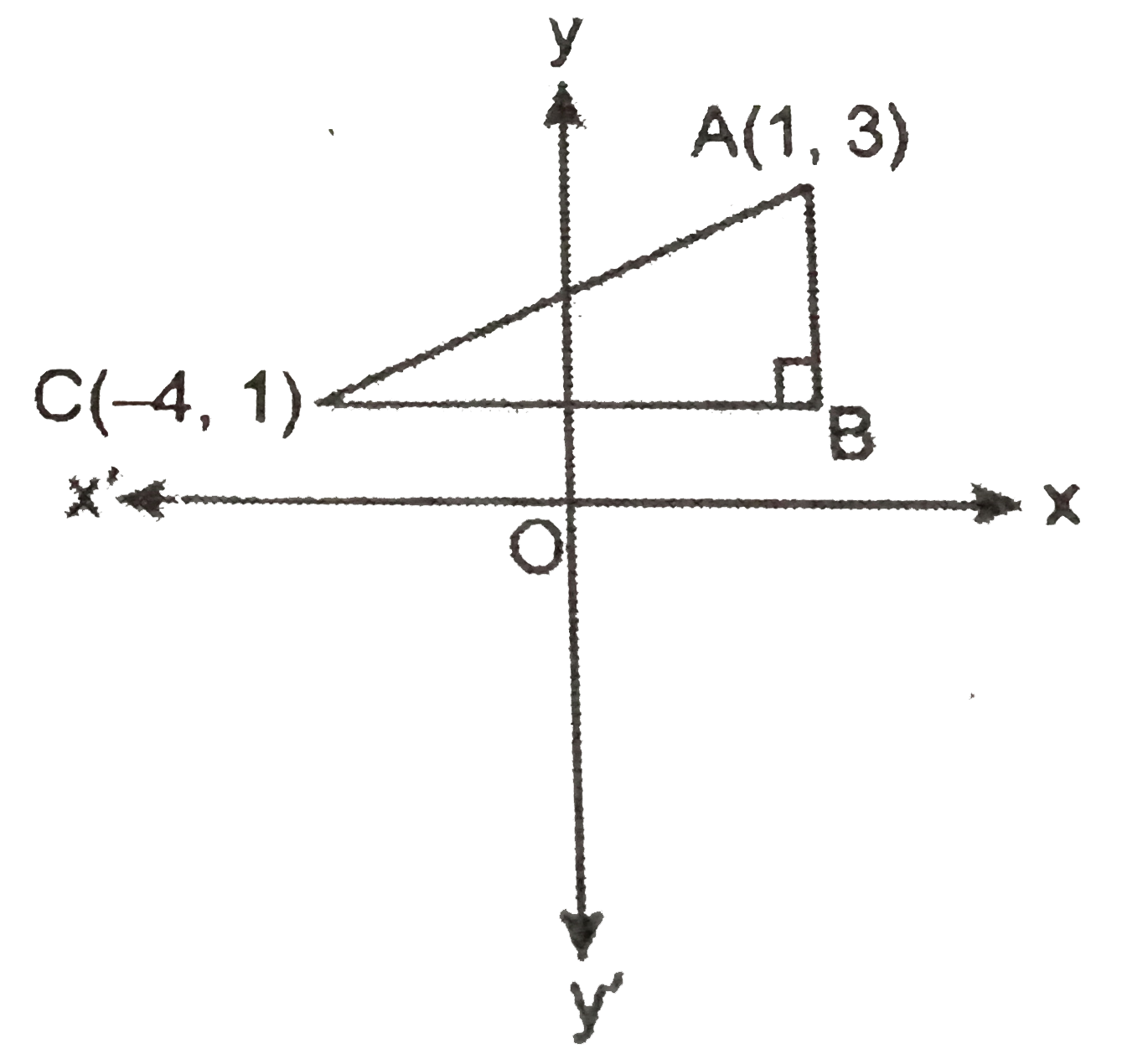
Let, in ΔABC
∠B=90∘
A≡(1,3)
and C≡(−4,1)
Equation of a line BC passing through C and parallel to x-axis is,
y=1
Similarly equation of a line AB passing through A and parallel to y-axis is
x=1
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
If the equation of the hypotenuse of a right - angled isosceles triangle is 3x+4y=4 and its opposite vertex is (2, 2), then the equations of the perpendicular and the base are respectively
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionThe hypotenuse of a right angled triangle is 45 cm long. If one of the legs of this triangle is 36 cm, then find the length of other leg.
View SolutionEquation of the base of an equilateral triangle is 3x+4y=9 and its vertex is at point (1,2) .Find the equations of the other sides and the length of each side of the triangle .
View SolutionThe mid-points of the sides of a triangle are (2,1),(−5,7)and(−5,−5). Find the equations of the sides of the triangle.
View Solutionthe hypotenuse of a right angle triangle is 1m less than twice the shortest side. If the third side is 1m more than the shortest side, find the sides of the triangle.
View SolutionThe legs of a right- angled triangle area in the ratio 5:12. If its ara is 120 sq. m, find the legs.
View SolutionProve that the points A(1, -3), B (-3, 0) and C(4, 1) are the vertices of an isosceles right- angled triangle. Find the area of the triangle.
View SolutionA circle touches the hypotenuse of a right angled triangle at its middle point and passes through the mid-point of the shorter side. If aandb(a<b) be the lengths of the sides, then prove that the radius of the circle is b4a√a2+b2
View SolutionProve that the points (−3, 0), (1, −3) and (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of this triangle.
View Solution

