Prove that the A.M. of two positive real numbers is greater than their G.M.
The correct Answer is:N/a
To prove that the Arithmetic Mean (A.M.) of two positive real numbers is greater than their Geometric Mean (G.M.), we will follow these steps:
Step 1: Define the two positive real numbers
Let the two positive real numbers be a and b.
Step 2: Calculate the Arithmetic Mean (A.M.)
The Arithmetic Mean of a and b is given by:
A.M.=a+b2
Step 3: Calculate the Geometric Mean (G.M.)
The Geometric Mean of a and b is given by:
G.M.=√ab
Step 4: Set up the inequality
We want to show that:
A.M.>G.M.
This translates to:
a+b2>√ab
Step 5: Rearranging the inequality
To eliminate the fraction, we can multiply both sides by 2 (since both a and b are positive, this does not change the direction of the inequality):
a+b>2√ab
Step 6: Square both sides
Next, we square both sides of the inequality to eliminate the square root:
(a+b)2>(2√ab)2
This simplifies to:
a2+2ab+b2>4ab
Step 7: Rearranging the terms
Now, we can rearrange the terms:
a2+b2+2ab−4ab>0
This simplifies to:
a2+b2−2ab>0
Step 8: Recognizing a perfect square
Notice that a2+b2−2ab can be rewritten as:
(a−b)2>0
Step 9: Conclusion
Since a and b are positive real numbers, (a−b)2 is always non-negative and is equal to zero only when a=b. Therefore, for a≠b, we have:
(a−b)2>0
This implies that:
A.M.>G.M.
Thus, we have proved that the Arithmetic Mean of two positive real numbers is greater than their Geometric Mean.
Let the two positive real numbers be a and b.
The Arithmetic Mean of a and b is given by:
A.M.=a+b2
The Geometric Mean of a and b is given by:
G.M.=√ab
We want to show that:
A.M.>G.M.
This translates to:
a+b2>√ab
To eliminate the fraction, we can multiply both sides by 2 (since both a and b are positive, this does not change the direction of the inequality):
a+b>2√ab
Next, we square both sides of the inequality to eliminate the square root:
(a+b)2>(2√ab)2
This simplifies to:
a2+2ab+b2>4ab
Now, we can rearrange the terms:
a2+b2+2ab−4ab>0
This simplifies to:
a2+b2−2ab>0
Notice that a2+b2−2ab can be rewritten as:
(a−b)2>0
Since a and b are positive real numbers, (a−b)2 is always non-negative and is equal to zero only when a=b. Therefore, for a≠b, we have:
(a−b)2>0
This implies that:
A.M.>G.M.
Thus, we have proved that the Arithmetic Mean of two positive real numbers is greater than their Geometric Mean.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9A4videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9B18videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
Similar Questions
Knowledge Check
- Question 1 - Select One
If r and s are two positive numbers and r is 25% greater than s, what is the value of the ratio r/s?
A0.75B0.8C1D1.25 - Question 2 - Select One
The zeros of the polynomial function g are 4 and -2. If the range of g is the set real numbers greater than or equal to -3, which of the following could be the graph of y=g(x) in the xy-plane?
A B
B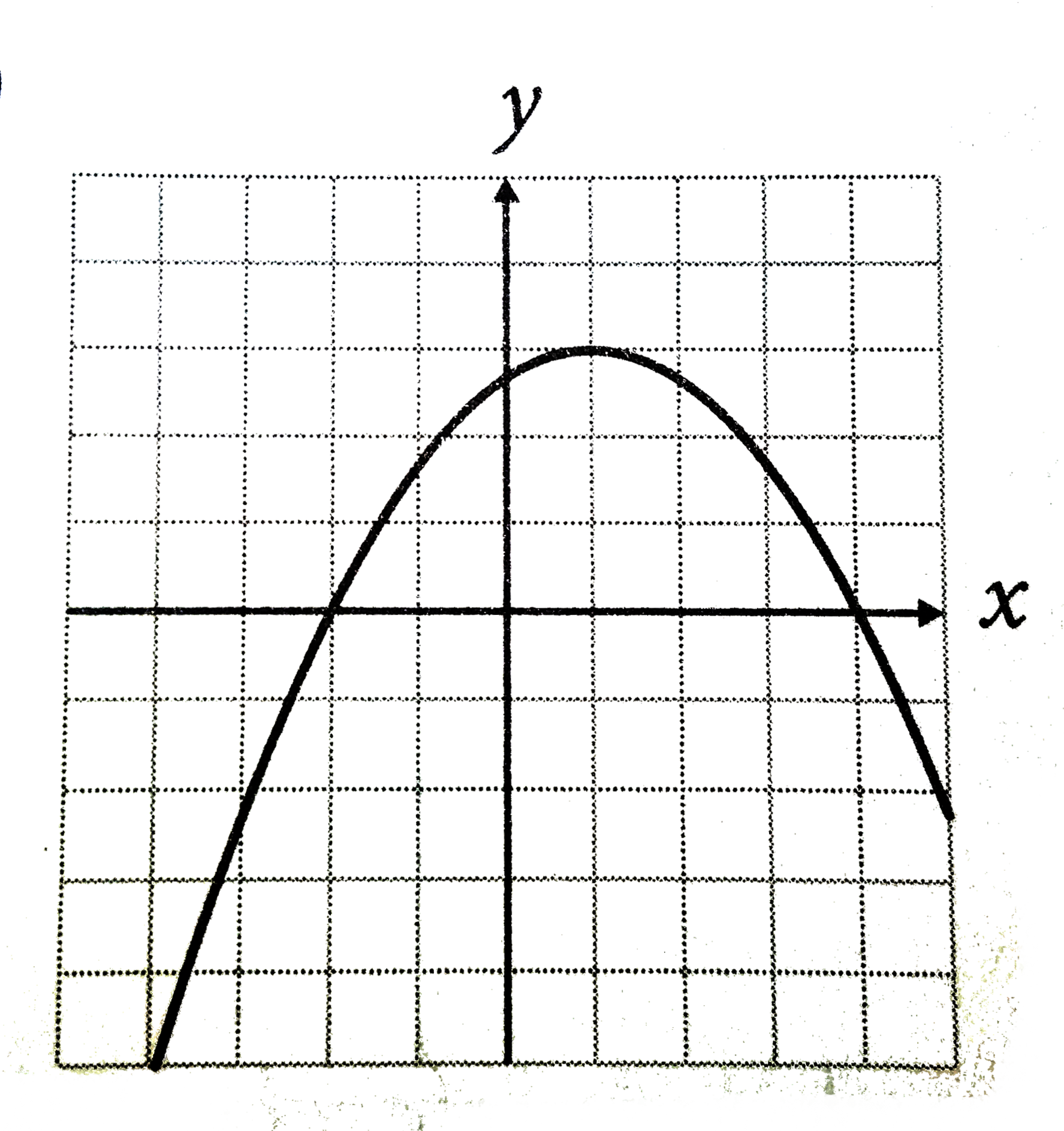 C
C D
D
If sum of the A.M.&G.M. of two positive distinct numbers is equal to the difference between the number then numbers are in ratio :
View SolutionIf the A.M. of two positive numbers aandb(a>b) is twice their geometric mean. Prove that : a:b=(2+√3):(2−√3).
View SolutionIf the A.M. of two positive numbers aandb(a>b) is twice their geometric mean. Prove that : a:b=(2+√3):(2−√3).
View SolutionIf the A.M. between two positive numbers exceeds their G.M. by 2 and the ratio of the numbers
be 1:4 find the numbers .View SolutionThe A.M of two numbers is 17 and their G.M. is 8. Find the numbers.
View SolutionThe ratio of the A.M. and G.M. of two positive numbers a and b, is m : n. Show that a : b = (m+√m2−n2):(m−√m2−n2).
View Solution

