In a G.P. it is given that Tp−1+Tp+1=3Tp. Prove that its common ratio is an irrational number.
To prove that the common ratio r of the given geometric progression (G.P.) is an irrational number, we start from the equation provided in the question:
Tp−1+Tp+1=3Tp
Step 1: Express the terms in terms of the first term and common ratio
In a G.P., the n-th term can be expressed as:
Tn=arn−1
where a is the first term and r is the common ratio. Therefore, we can express the terms Tp−1, Tp, and Tp+1 as follows:
Tp−1=arp−2,Tp=arp−1,Tp+1=arp
Step 2: Substitute these expressions into the equation
Substituting these expressions into the given equation:
arp−2+arp=3arp−1
Step 3: Factor out a (assuming a≠0)
Dividing the entire equation by a (since a≠0) gives:
rp−2+rp=3rp−1
Step 4: Rearrange the equation
Rearranging the equation, we have:
rp−2+rp−3rp−1=0
Step 5: Factor out rp−2
Factoring out rp−2:
rp−2(1+r2−3r)=0
Since rp−2≠0 (assuming r≠0), we can simplify to:
1+r2−3r=0
Step 6: Rearranging to standard quadratic form
Rearranging gives us the standard quadratic equation:
r2−3r+1=0
Step 7: Use the quadratic formula to find r
Using the quadratic formula r=−b±√b2−4ac2a where a=1,b=−3,c=1:
r=3±√(−3)2−4⋅1⋅12⋅1
Calculating the discriminant:
r=3±√9−42=3±√52
Step 8: Determine if r is rational or irrational
The terms 3+√5 and 3−√5 are both irrational since √5 is irrational. Therefore, both values of r:
r=3+√52andr=3−√52
are irrational numbers.
Conclusion
Thus, we have proved that the common ratio r of the given geometric progression is indeed an irrational number.
---
In a G.P., the n-th term can be expressed as:
Substituting these expressions into the given equation:
Dividing the entire equation by a (since a≠0) gives:
Rearranging the equation, we have:
Factoring out rp−2:
Rearranging gives us the standard quadratic equation:
Using the quadratic formula r=−b±√b2−4ac2a where a=1,b=−3,c=1:
The terms 3+√5 and 3−√5 are both irrational since √5 is irrational. Therefore, both values of r:
Thus, we have proved that the common ratio r of the given geometric progression is indeed an irrational number.
Topper's Solved these Questions
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9G
17 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9H
9 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9E
15 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
12 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise
16 Videos
Similar Questions
Knowledge Check
If the first term of a G.P. a1,a2,a3 is unity such that 4a2+5a3 is least, then the common ratio of the G.P. is
A25B−25C−35D−15For a given exothermic reaction ,KPandKp' are the equilibrium constant at temperature T1andT2 respectively .Assuming that heat of reaction is constant in temperature range between T1andT2 , it is readly observed that
AKp>KpBKp<KpCKp=KpDKp=1Kp'
Prove that for any prime positive integer p,√p is an irrational number.
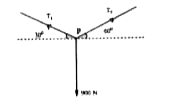
View SolutionIf 'P' is in equilibrium then T1/T2 is
View SolutionThe % yield of ammonia as a function of time in the reaction, N2(g)+3H2(g)⇔2NH3(g)'ΔH<0
at (p,T1) is given below
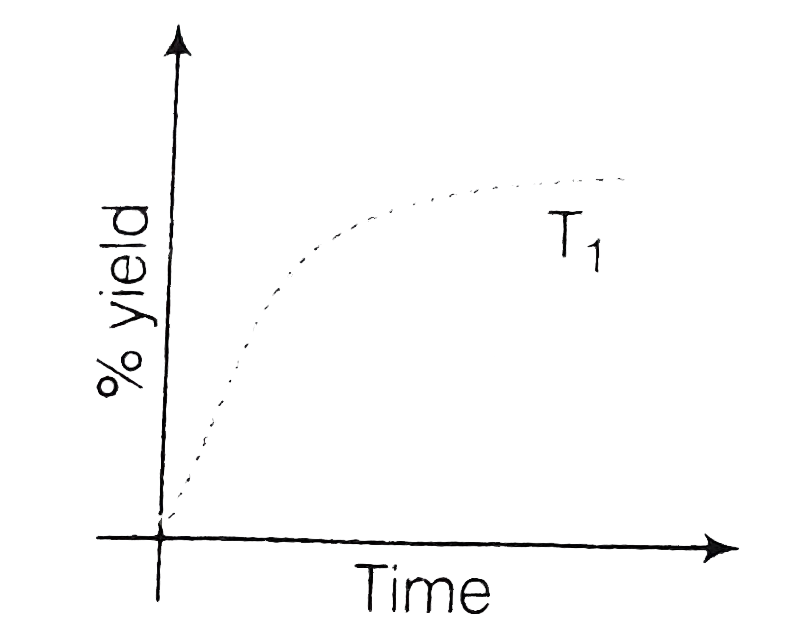
If this reaction is conducted at (p,T1), with T2>T1 the % yield by of ammonia as a function of time is represented by
View SolutionThe nth term of a progression is 2n. Prove that it is G.P. Also find its common ratio.
View SolutionFind the 12thterm of a G.P. whose 8th term is 192 and the common ratio is 2.
View SolutionIn an A,P if the pth term is 1qandqth terms is 1p. Prove that the sum of first pq term is 12 (pq+1) where, (p≠q)
View Solution
