−12<4−3x−5≤2
The correct Answer is:N/a
To solve the inequality −12<4−3x−5≤2, we will break it down step by step.
Step 1: Rewrite the Inequality
The given inequality is:
−12<4−3x−5≤2
Since −3x−5 is the same as 3x5, we can rewrite the inequality as:
−12<4+3x5≤2
Step 2: Split the Compound Inequality
We can split the compound inequality into two parts:
1. −12<4+3x5
2. 4+3x5≤2
Step 3: Solve the First Inequality
Starting with the first part:
−12<4+3x5
Subtract 4 from both sides:
−12−4<3x5
This simplifies to:
−16<3x5
Now, multiply both sides by 5 to eliminate the fraction:
−80<3x
Finally, divide by 3:
−803<x
Step 4: Solve the Second Inequality
Now, let's solve the second part:
4+3x5≤2
Subtract 4 from both sides:
3x5≤2−4
This simplifies to:
3x5≤−2
Multiply both sides by 5:
3x≤−10
Finally, divide by 3:
x≤−103
Step 5: Combine the Results
Now we have two inequalities:
1. x>−803
2. x≤−103
Combining these gives:
−803<x≤−103
Final Answer
Thus, the solution set is:
x∈(−803,−103)
---
The given inequality is:
−12<4−3x−5≤2
Since −3x−5 is the same as 3x5, we can rewrite the inequality as:
−12<4+3x5≤2
We can split the compound inequality into two parts:
1. −12<4+3x5
2. 4+3x5≤2
Starting with the first part:
−12<4+3x5
Subtract 4 from both sides:
−12−4<3x5
This simplifies to:
−16<3x5
Now, multiply both sides by 5 to eliminate the fraction:
−80<3x
Finally, divide by 3:
−803<x
Now, let's solve the second part:
4+3x5≤2
Subtract 4 from both sides:
3x5≤2−4
This simplifies to:
3x5≤−2
Multiply both sides by 5:
3x≤−10
Finally, divide by 3:
x≤−103
Now we have two inequalities:
1. x>−803
2. x≤−103
−803<x≤−103
Thus, the solution set is:
x∈(−803,−103)
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - NCERT QUESTION
51 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- MATHEMATICAL REASONING BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise
7 Videos
Similar Questions
Knowledge Check
The solution set of 3x5+2<x+4≤x2+5,x∈R on the number line is:
A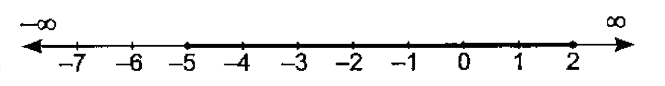 B
B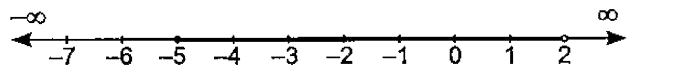 C
C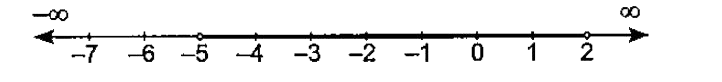 D
D
Solve the following inequation and represent the solution set on the number line :
4x−19<3x5−2≤−25+x,∈R
View SolutionSolve the inequalities : −12<4−3x−5≤2
View SolutionSolve the inequation : −12≤4−3x−5x+2
View SolutionSolve the following inequlaities
7x+15≥9−4x
−5≤2−3x4≤9
5x−6≤4 and 7−3x≥2x
View Solution−5≤2−3x4≤9
View SolutionA function f is defined on the set of real numbers as follows:
f(x)=⎧⎪⎨⎪⎩x+11≤x<22x−12≤x<43x−104≤x<6
(a) Find the domain of the function.
(b) Find the range of the function.
View SolutionIf f(x)=⎧⎨⎩√4+ax−√4−axx−1≤x<03x+2x−80≤x≤1 continuous in [−1,1], then the value of a is
View Solution
