In the following cases, find the distance of each of the given points from the corresponding given plane.
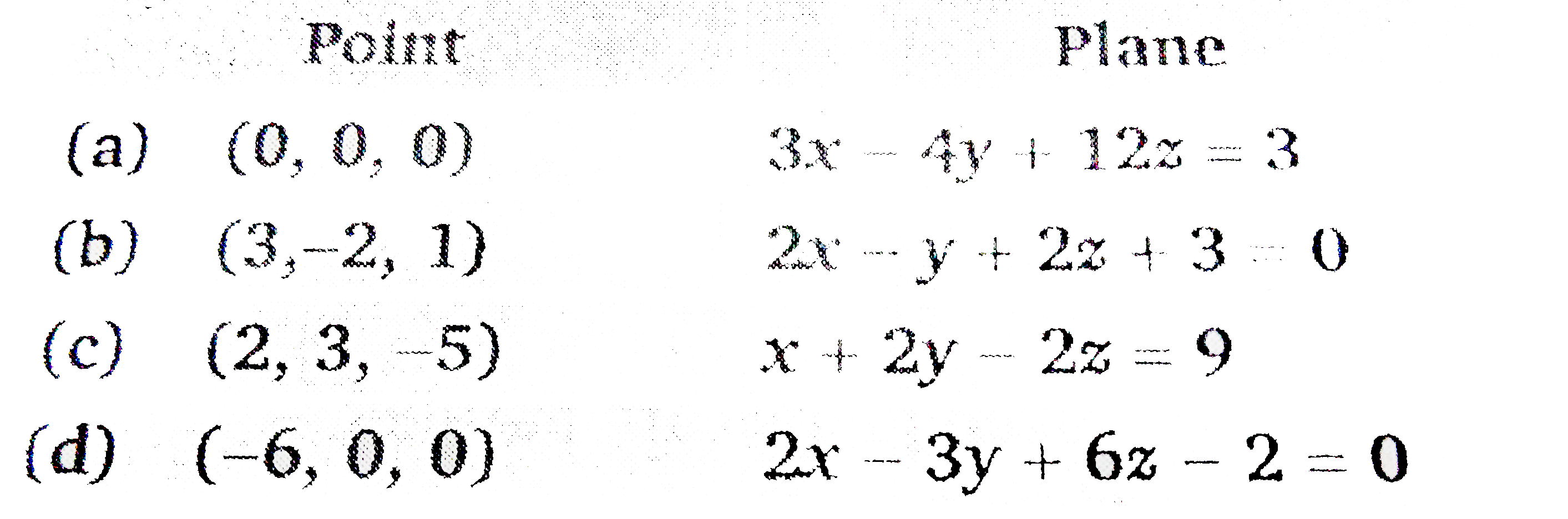
We know that the distance of point P(x1,y1,z1) to the plane Ax+By+Cz=D is
d=∣∣∣Ax1+By1+Cz1−D√A2+B2+C2∣∣∣………(i)
(a) Distance of point (0,0,0) from the plane 3x−4y+12z−3=0 is
d=|3×0−4×0+12×0−3|√32+(−4)2+(122)=|−3|√9+16+144
=3√169=313 unit
(b) Distance of point (3,−2,1) from the plane 2x−y+2z+3=0 is
d=|2×3+(−1)×(−2)+2×1+3|√22+(−1)2+22
=|6+2+2+3|√4+1+4
=13√9=133 unit
(c) Distance of point (2,3,−5) from the plane x+2y−2z−9=0 is
d=|2+2×3−2×(−5)−9|√12+22+(−2)2=|2+6+10−9|√1+4+4
=9√9=93=3 unit
(d) Distance of point (-6,0,0) from the plane 2x−3y+6z−2=0 is
d=|2×(−6)−3×0+6×0−2|√22+(−3)2+62=|−14|√4+9+36
=147=2 unit.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Miscellaneous Exercise
23 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 11.2
17 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
- VECTORSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VECTORSEXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
Find the distance of each of the following points from the corresponding given plane: (0,0,0),3x−4y+12z=3
View SolutionFind the distance of each of the following points from the corresponding given plane: (2,3,−5),x+2y−2z=9
View SolutionFind the distance of each of the following points from the corresponding given plane: (−6,0,0),2x−3y+6z−2=0
View SolutionFind the distance of each of the following points from the corresponding given plane: (3,−2,1),(2x−y+2z+3=0
View SolutionFind the distance of the point (2, 3, 5) from the xy-plane.
View SolutionFind the distances of the point P(2, 3, 2) from the
coordinate planes.
View SolutionFind the distance of the point (21,0) from the plane 2x+y+2z+5=0.
View SolutionIn each of the following cases,determine the direction cosines of the normal to the plane ned its distance from the origin: 5y+8=0
View SolutionShow that the relation R in the set A of points in a plane given by R={(P,Q):distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set o
View SolutionFind the distance from the origin to each of the point:
(2,2,3)
View Solution
