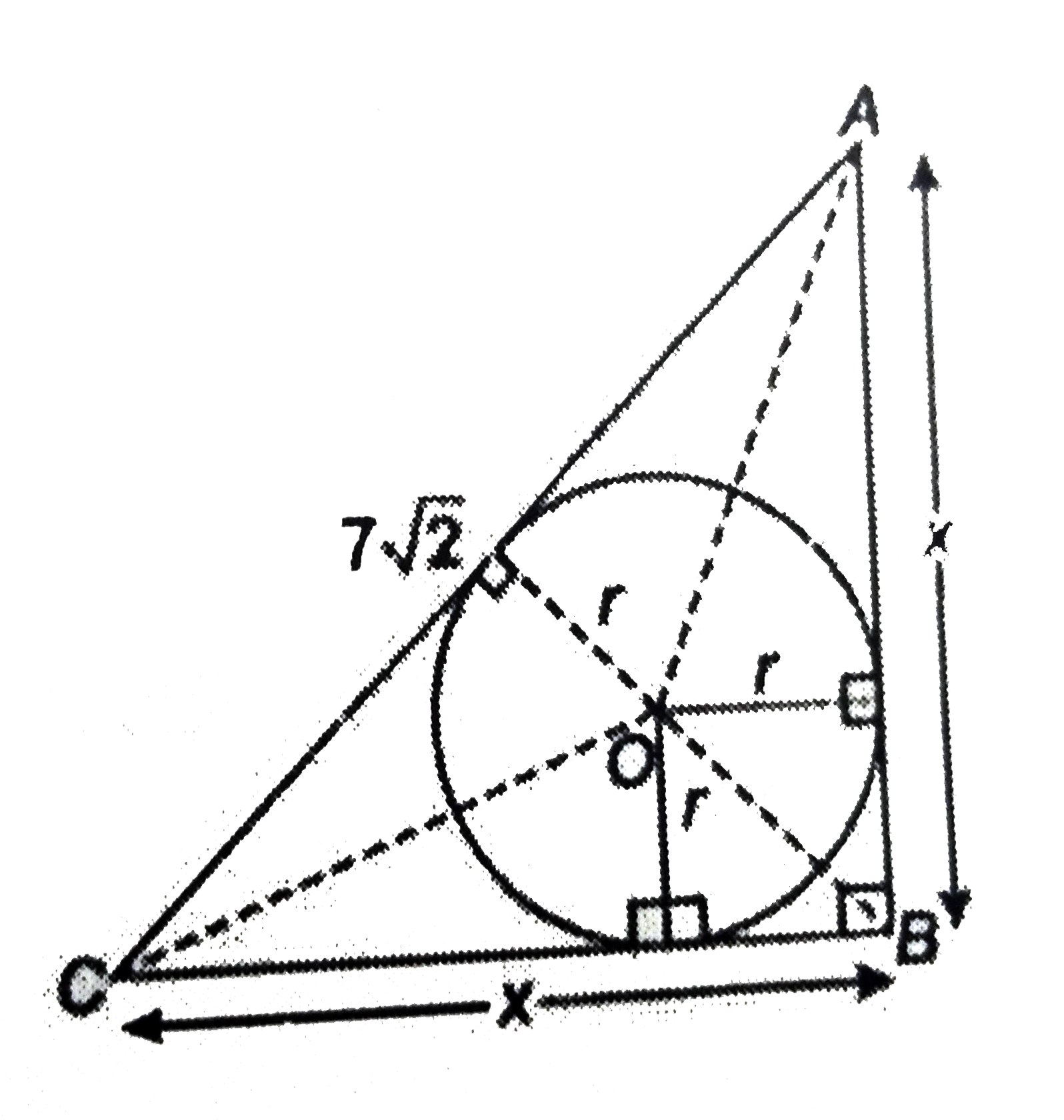
If the hypotenuse of an isosceles right triangle is $7 \sqrt{2}$ cm, find the area of the circle inscribed in it

Video Solution

Text Solution

Verified by Experts

Let AB = BC = x cm
$∴$ In right $Δ A B C$ , by Pythagoras theorem
$x^{2} + x^{2} = {(7 \sqrt{2})}^{2}$
$\Rightarrow 2 x^{2} = 98 \Rightarrow x^{2} = 49 \Rightarrow x = 7 c m$
$∴ A r (Δ A B C) = a r (Δ A O B) + a r (Δ B O C) + a r (Δ C O A)$
$\frac{1}{2} \times x \times x = \frac{1}{2} \times x \times r + \frac{1}{2} \times 7 \sqrt{2} \times r$
$\Rightarrow 7 \times 7 = 7 \times r + 7 \times r + 7 \sqrt{2} \times r \Rightarrow r = \frac{7}{2 + \sqrt{2}}$
$\Rightarrow r = \frac{7}{2 + \sqrt{2}} \times \frac{2 - \sqrt{2}}{2 - \sqrt{2}} = \frac{7 (2 - \sqrt{2})}{2}$
$∴$ Area of circle $= π r^{2}$
$= \frac{22}{7} \times \frac{49 {(2 - \sqrt{2})}^{2}}{4} = \frac{77}{2} \times (4 + 2 - 4 \sqrt{2})$
$= 77 (3 - 2 \sqrt{2}) c m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-AREA RELATED TO CIRCLES-Problems From NCERT /exemplar

Home
Ask Doubt
Profile