A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77cm (figure). Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/s. Calculate the number of complete revolutions the wheel makes in raising the bucket.
The correct Answer is:40
Step by step video & image solution for A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77cm (figure). Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/s. Calculate the number of complete revolutions the wheel makes in raising the bucket. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
12 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Problems From NCERT /exemplar
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
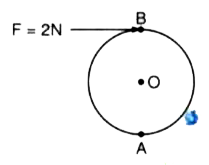
View SolutionA wheel of diameter 2m is shown in Fig 1.28 with axle at O. At force F= 2N is applied at B in the direction shown in figure, Calculate the moment of force about (i) the centre O, and (ii) the point A.
View SolutionA cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 ms−1. Calculate, in minutes, the time it takes to fill the tank
View SolutionFigure shows water in a container having 2.0−mm thick walls made of a material of thermal conductivity 0.50Wm−1C−1 . The container is kept in a melting-ice bath at 0∘C . The total surface area in contact with water is0.05m2 . A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10cms−1 and the temperature of the water remains constant at 1.0∘C .Find the mass M of the block. Assume that the heat flow out of the water only through the walls in contact. Take g=10ms−2 .

View SolutionA car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
View SolutionOne end of a string is tied to a rigid support attached to roof and the other end is wound around a uniform wheel of radius r and mass m. The string is kept vertical and the wheel is released from rest. As the wheel descends show that (i) the tension in the string is one-third the weight of the wheel, (ii) the magnitude of the acceleration of the centre of mass is 2g/3 and (iii) the speed of the centre of mass is (4gh/3)1/2

View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
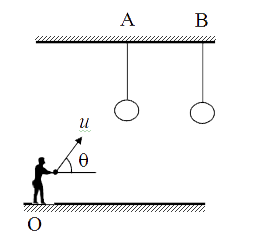
The projection speed of the ball is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.

The projection speed of the ball is:
View SolutionA boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
View SolutionA boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
View Solution
