A sector is cut from a circle of radius 21 cm. The angle of the sector is 150∘. Find its area
The correct Answer is:577.5cm2
To find the area of a sector of a circle, we can use the formula:
Area of Sector=θ360×πr2
where:
- θ is the angle of the sector in degrees,
- r is the radius of the circle,
- π is a constant approximately equal to 3.14 or can be taken as 227 for calculations.
Given:
- Radius r=21cm
- Angle θ=150∘
Step 1: Substitute the values into the formula
Area of Sector=150360×227×(21)2
Step 2: Calculate (21)2
(21)2=441
Step 3: Substitute (21)2 back into the area formula
Area of Sector=150360×227×441
Step 4: Simplify 150360
150360=512
Step 5: Substitute the simplified fraction back into the area formula
Area of Sector=512×227×441
Step 6: Calculate 227×441
227×441=22×4417=22×63=1386
Step 7: Substitute this value back into the area formula
Area of Sector=512×1386
Step 8: Calculate 5×138612
5×1386=6930
Now divide by 12:
693012=577.5
Final Answer
The area of the sector is:
Area of Sector=577.5cm2
- θ is the angle of the sector in degrees,
- r is the radius of the circle,
- π is a constant approximately equal to 3.14 or can be taken as 227 for calculations.
- Radius r=21cm
- Angle θ=150∘
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Short Answer Question
12 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
5 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
A sector is cut off from a circle of radius 21 cm. The angle of the sector is 150∘. Find the length of its arc and the area.
View SolutionA sector is cut from a circle of radius 21 cm. The angle of the sector is 150 degree . Find the length of its arc and area.
View SolutionA sector is cut-off from a circle of radius 21 cm. The angle of the sector is 120o . Find the length of its arc and the area.
View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘
View SolutionFind the area of the minor segment of a circle of radius 14cm, when the angle of the corresponding sector is 60∘

View SolutionThe radius of a circle is 14 cm and the area of the sector is 102.7cm2. Find the central angle of the sector.
View SolutionA chord AB of a circle, of radius 14 cm makes an angle of 60∘ at the centre of the circle. Find the area of the minor segment of the circle.
View SolutionThe central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120∘and40∘ . Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe ?
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
(i) minor segment
(ii) major sector.
View SolutionWhat is the area of the sector shown in
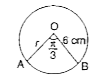
View Solution
