A line segment AB is 8 cm in length. AB is produced to P such that BP2=AB.AP, find the length of BP.
The correct Answer is:4(√5+1)cm
To solve the problem, we need to find the length of BP given that BP2=AB⋅AP and AB=8 cm.
1. Define the Variables:
Let BP=x cm. Since AB=8 cm, we can express AP in terms of x:
AP=AB+BP=8+x
2. Set Up the Equation:
According to the problem, we have:
BP2=AB⋅AP
Substituting the values we have:
x2=8⋅(8+x)
3. Expand the Equation:
Expanding the right-hand side:
x2=64+8x
4. Rearrange the Equation:
Rearranging the equation gives us:
x2−8x−64=0
5. Use the Quadratic Formula:
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1, b=−8, and c=−64.
6. Calculate the Discriminant:
First, calculate the discriminant:
b2−4ac=(−8)2−4⋅1⋅(−64)=64+256=320
7. Substitute into the Quadratic Formula:
Now substituting back into the formula:
x=8±√3202
8. Simplify the Square Root:
Simplifying √320:
√320=√64⋅5=8√5
So, we have:
x=8±8√52
Simplifying further:
x=4±4√5
9. Determine the Length of BP:
Since length cannot be negative, we take the positive value:
BP=4(1+√5) cm
Final Answer:
The length of BP is 4(1+√5) cm.
Let BP=x cm. Since AB=8 cm, we can express AP in terms of x:
AP=AB+BP=8+x
According to the problem, we have:
BP2=AB⋅AP
Substituting the values we have:
x2=8⋅(8+x)
Expanding the right-hand side:
x2=64+8x
Rearranging the equation gives us:
x2−8x−64=0
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1, b=−8, and c=−64.
First, calculate the discriminant:
b2−4ac=(−8)2−4⋅1⋅(−64)=64+256=320
Now substituting back into the formula:
x=8±√3202
Simplifying √320:
√320=√64⋅5=8√5
So, we have:
x=8±8√52
Simplifying further:
x=4±4√5
Since length cannot be negative, we take the positive value:
BP=4(1+√5) cm
The length of BP is 4(1+√5) cm.
Topper's Solved these Questions
- QUADRATIC EQUATIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Very Short Answer Questions
15 Videos
- QUADRATIC EQUATIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Short Answer Questions
10 Videos
- QUADRATIC EQUATIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRATIC EQUATIONSEXERCISE - Exercise 4c
12 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise Very Short Answer/short Answer Questions
16 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
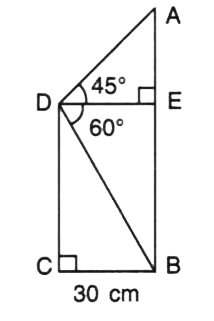
Find the length of AB.
View SolutionDraw a line segment AB = 4 cm . Now construct another line segment PQ such that PQ is thrice the length of AB. Verify your construction by measuring PQ with a ruler.
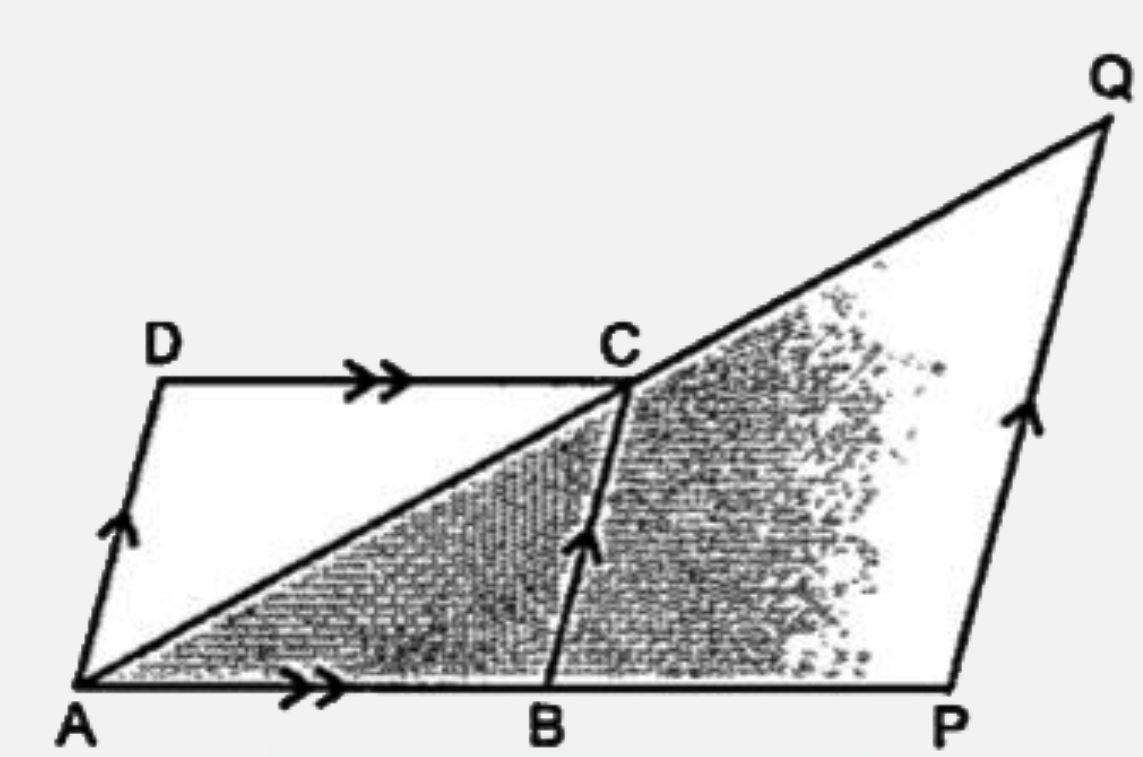
View SolutionIn the given figure, ABCD is a parallelogram. AB is produced to P, such that AB=BPandPQ is drawn parallel to BC to meet AC produced at Q. Given AB=8cm,AD=5cm,AC=10cm.
Find the perimeter of quadrilateral BCQP.
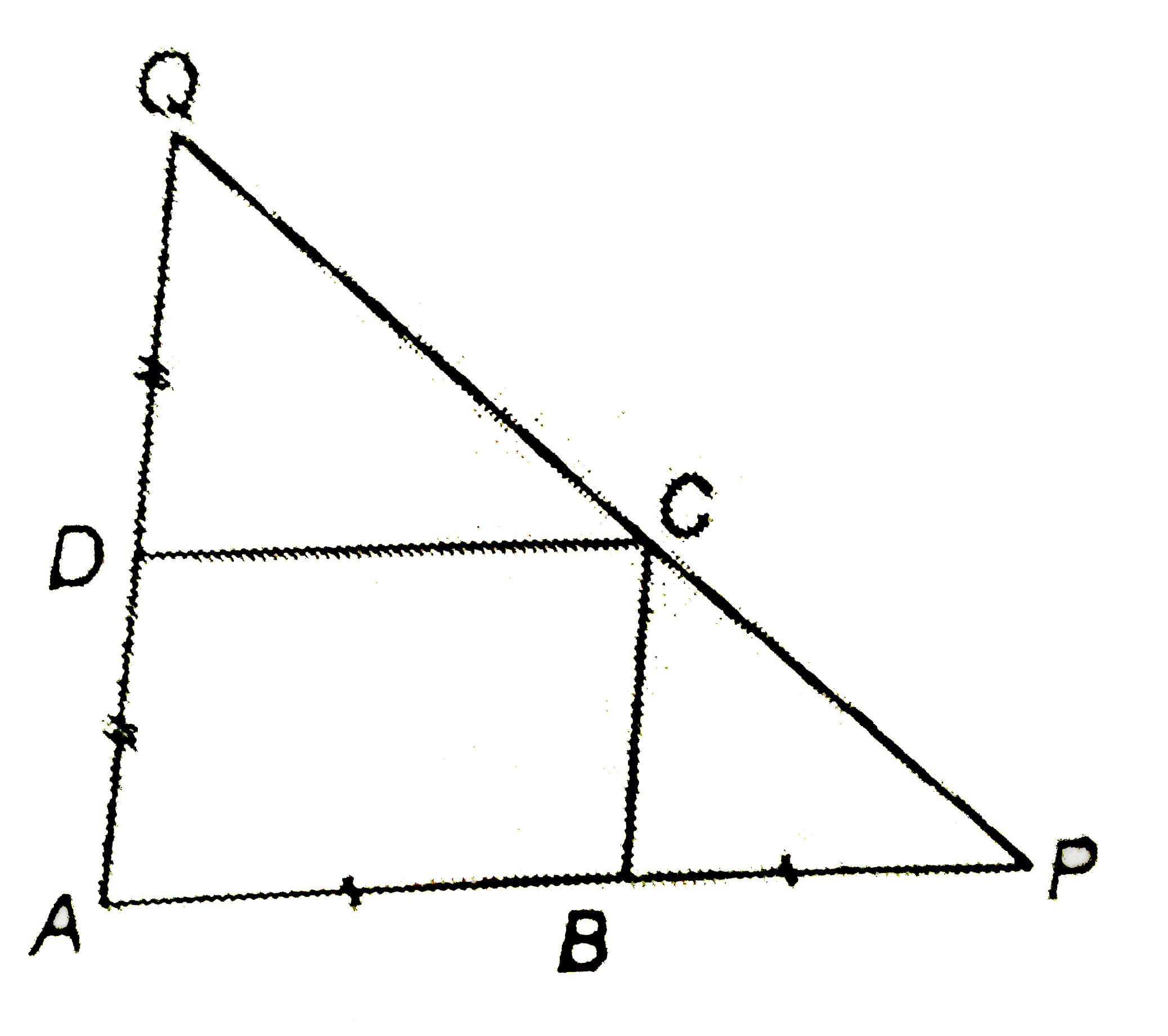
View SolutionIn the adjoining figure, ABCD is a paralogram. The side AB is produced to P such that AB=BP and the side AD is produced to Q such that AD = DQ. Prove that CP = CQ.
View SolutionDraw a line segment AB of length 5 cm using a ruler.
View SolutionIn the given figure, ABCD is a parallelogram. AB is produced to P, such that AB=BPandPQ is drawn parallel to BC to meet AC produced at Q. Given AB=8cm,AD=5cm,AC=10cm.
Prove that point C is mid-point of AQ.

View SolutionIn Figure, AB∣∣QR . Find the length of PB .
View SolutionDraw a line segment AB of length 5 cm using ruler and compass
View SolutionIf the equal sides ABandAC each of whose length is 2a of a righ aisosceles triangle ABC be produced to P and so that BP.CQ=AB, the line PQ always passes through the fixed point
View SolutionIf the equal sides AB and AC (each equal to 5 units) of a right-angled isosceles triangle ABC are produced to P and Q such that BP⋅CQ=AB2, then the line PQ always passes through the fixed point (where A is the origin and AB, AC lie along the positive x and positive y - axis respectively)
View Solution
