Question

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Explanation

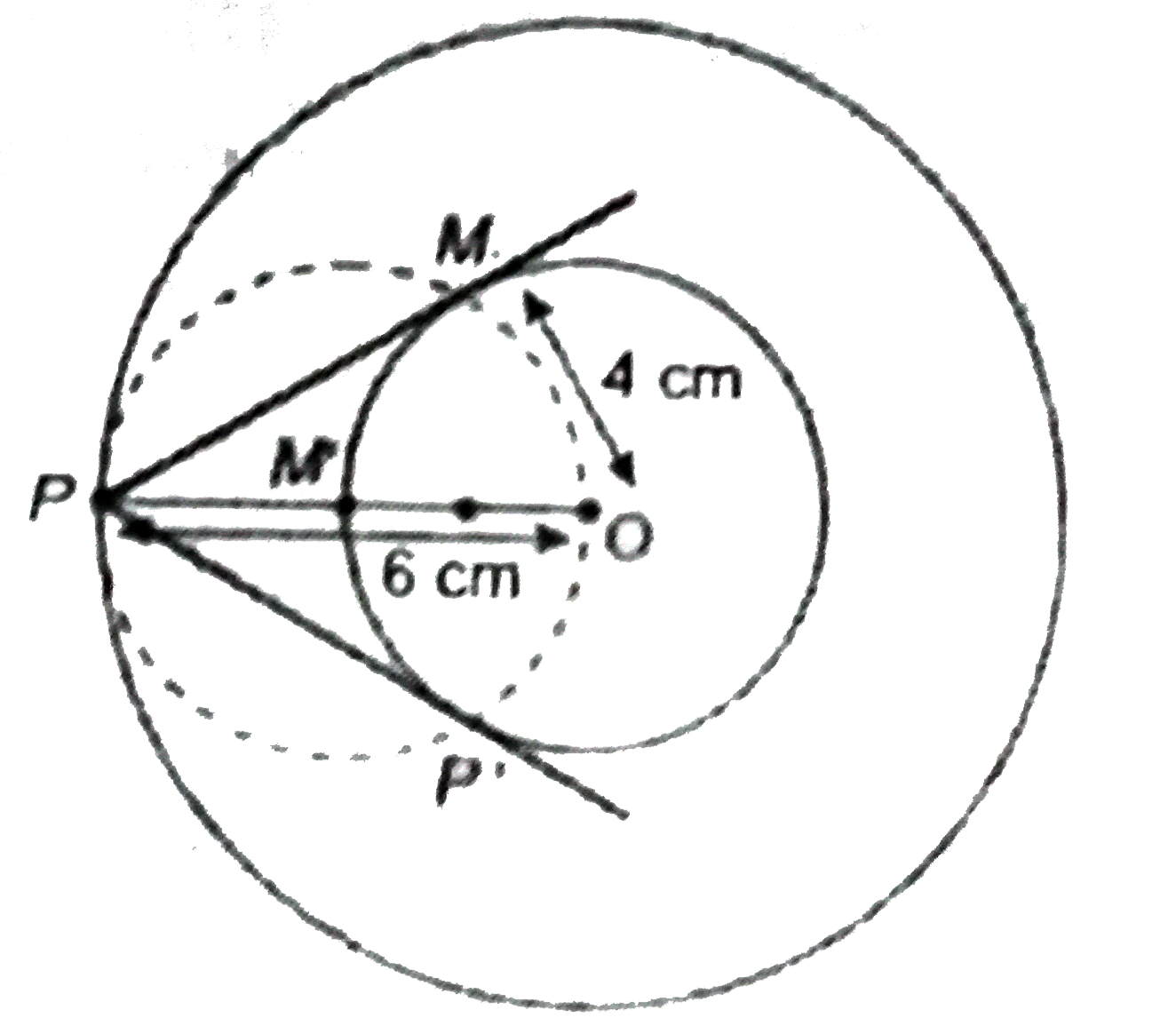
Given, two concentric circles of radill 4 cm and 6 cm with common centre O. We have to draw two tangents to inner circle from a point of outer circle.
Steps of Construction :
1. Draw two concentric circles with centre a O and radii 4 cm and 6 cm.
2. Take any point P on outer circle. Join OP.
3. Now, bisect OP. Let M' be the mid-point of OP.
3. Now, bisect OP. Let M' be the mid-point of OP. Taking M' as centre and OM' as radius draw a circle (dotted) which cuts the inner circle at M and P'.
4. Join PM and PP'. Thus, PM and PP' are required tangents.
5. On measuting PM and PP', we get PM = PP' = 4.47 cm.
Calculation :
In right `DeltaOMP,anglePMO=90^(@)`
`therefore" "PM^(2)=OP^(2)-OM^(2)" "("by Pythagoras theorem")`
`implies" "PM^(2)=(6)^(2)-(4)^(2)=36-16=20`
`implies" "PM=sqrt20=44.47`
Hence, the lenght of tangent is `4.47.`
Justification : Join OM and OP' which are radius.
The `angle OMP` is an angle lies in the semi-circle and therefore `angleOMP=90^(@)`
`implies " "OMbotOP`
Since, Om is radius of the circle, so MP has to be a tangent to the circle. Similarly, PP' is also a tangent to the circle.