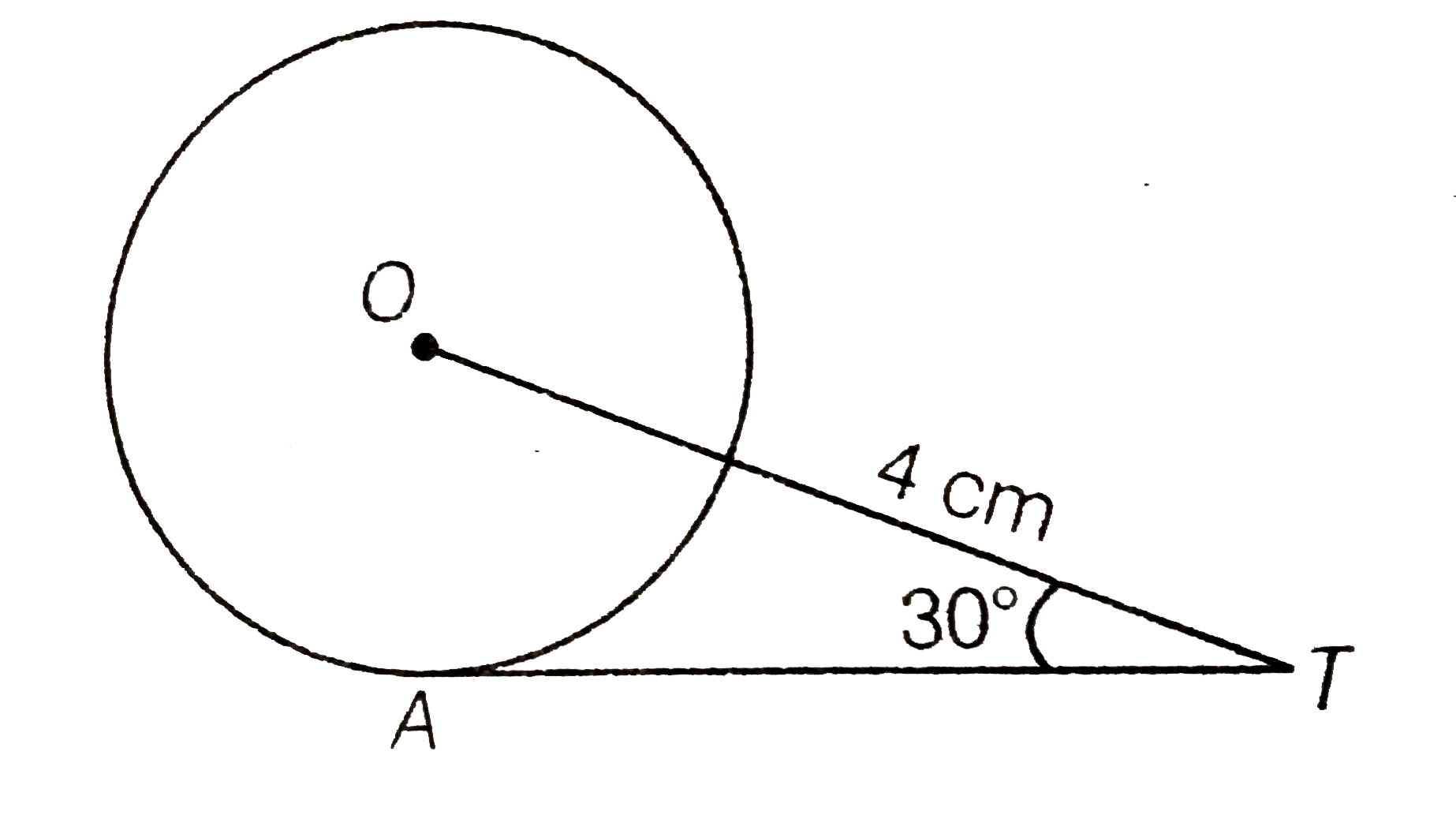
In the giben figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠PTA=30∘. Find the length of segment AT.

In right △OAT,
cos30∘=ATOT
⇒ √32=AT4 ⇒AT=2√3cm
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar11videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise32videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions10videos
CO-ORDINATE GEOMETRY
Similar Questions
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA=30∘. Then, AT is equal to
 View Solution
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
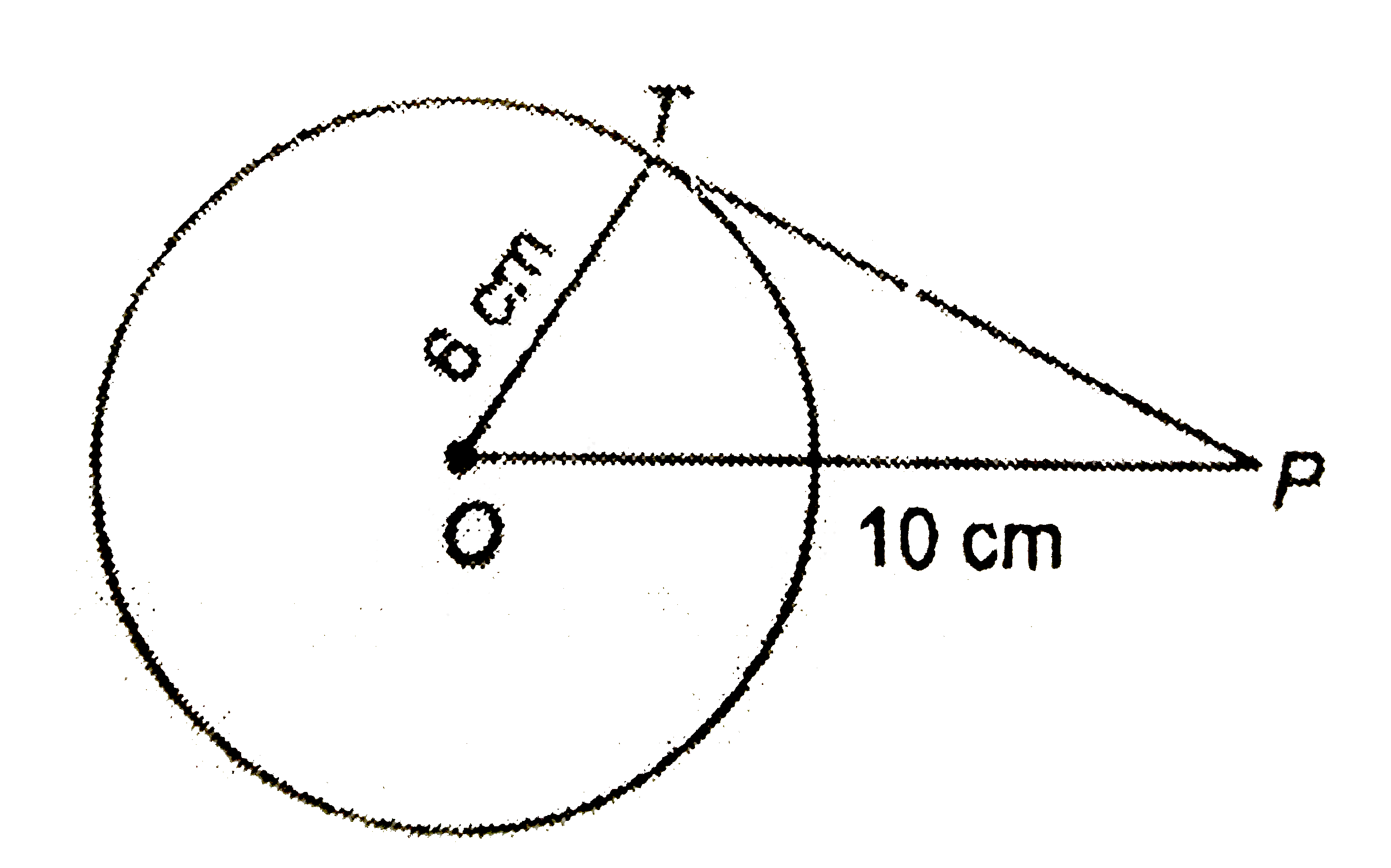 View Solution
View SolutionIn the given figure, PA and PB are tangents to a circle from an external point P such that PA=4 cm and ∠BAC=135∘. Find the length of dhord AB.
 View Solution
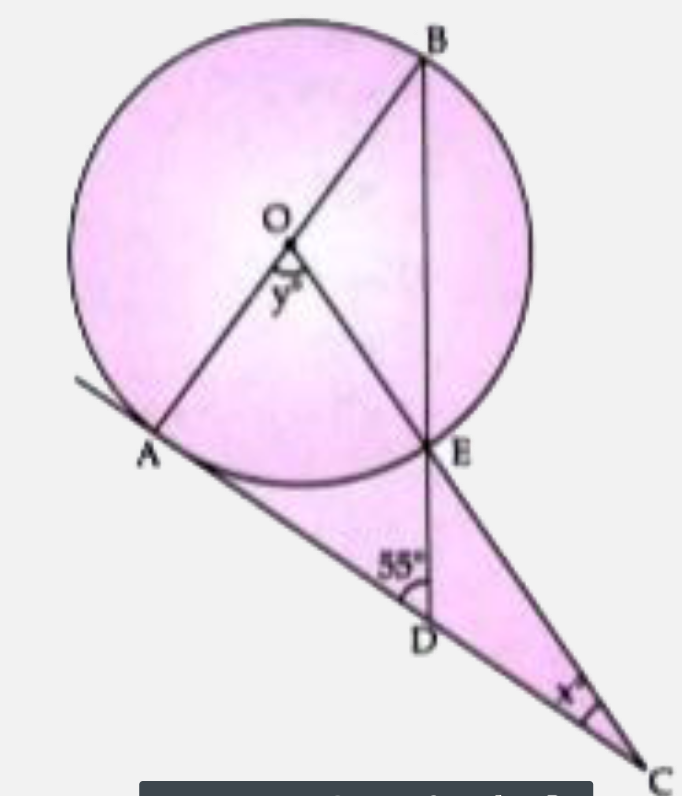
View SolutionIn the given figure AC is a tangent to the circle with centre O.
If ∠ADB=55∘, find x and y. Give reason for your answer.
 View Solution
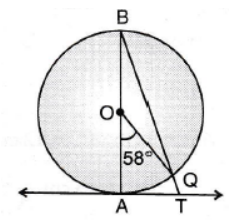
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
 View Solution
View SolutionIf PT is a tangent at T to a circle whose centre is O and OP=17cm , OT=8cm , Find the length of the tangent segment PT .
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
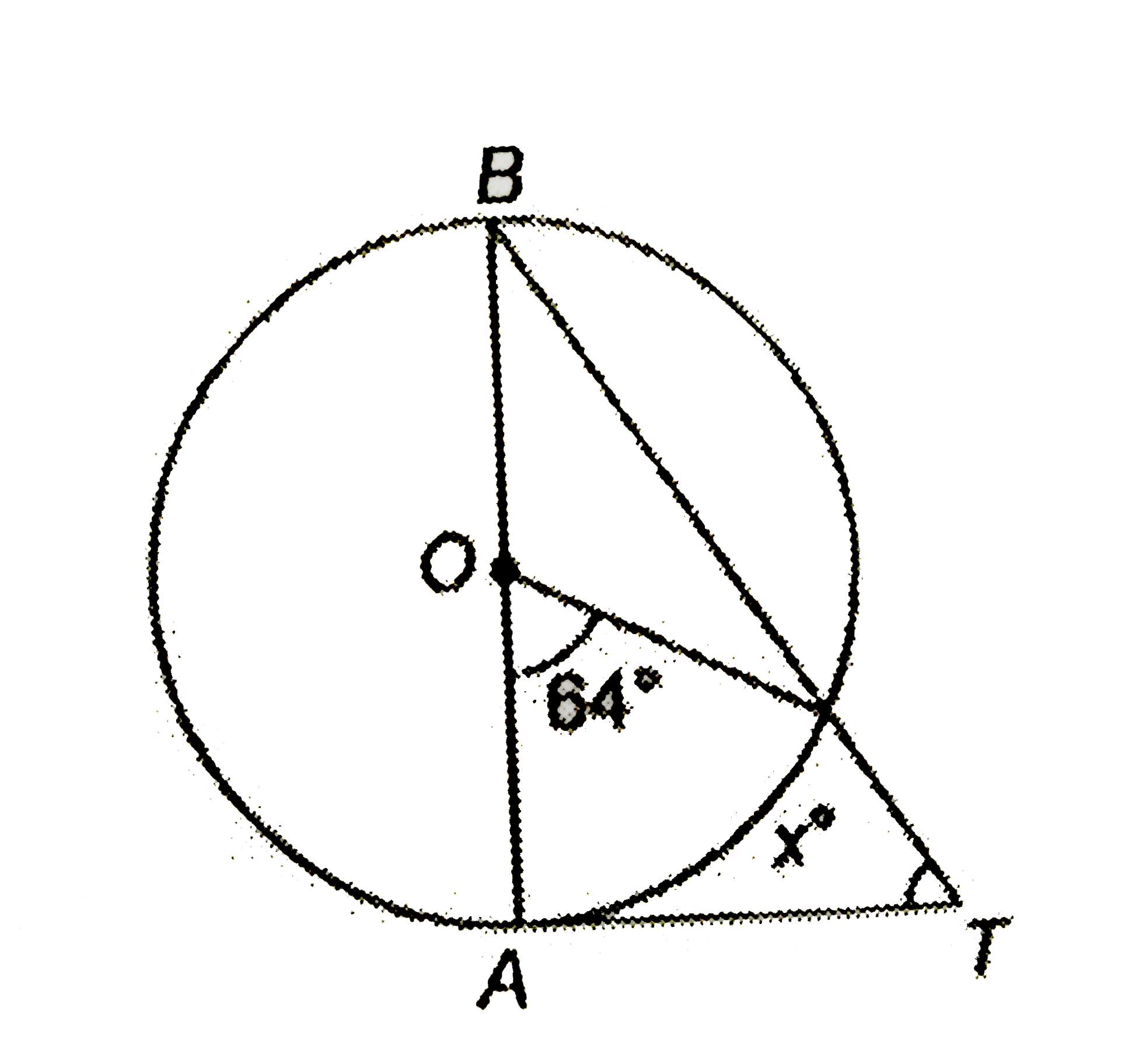
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
 View Solution
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
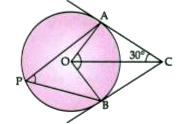
∠BCOView SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
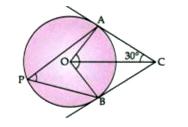
∠AOBView Solution

