Show that the points (-3, 2), (2, -3) and (1, 2√3) lie on the circumference of that circle, whose centre is origin.
To show that the points (-3, 2), (2, -3), and (1, 2√3) lie on the circumference of a circle whose center is at the origin (0, 0), we need to calculate the distance of each point from the origin and check if these distances are equal. The distance formula between two points (x1, y1) and (x2, y2) is given by:
d=√(x2−x1)2+(y2−y1)2
Step 1: Calculate the distance from the origin to the point (-3, 2)
Using the distance formula, we have:
d1=√(−3−0)2+(2−0)2
d1=√(−3)2+(2)2
d1=√9+4
d1=√13
Step 2: Calculate the distance from the origin to the point (2, -3)
Using the distance formula again:
d2=√(2−0)2+(−3−0)2
d2=√(2)2+(−3)2
d2=√4+9
d2=√13
Step 3: Calculate the distance from the origin to the point (1, 2√3)
Using the distance formula once more:
d3=√(1−0)2+(2√3−0)2
d3=√(1)2+(2√3)2
d3=√1+4⋅3
d3=√1+12
d3=√13
Conclusion
We have found that:
- Distance from the origin to (-3, 2) is √13
- Distance from the origin to (2, -3) is √13
- Distance from the origin to (1, 2√3) is √13
Since all three distances are equal to √13, we can conclude that the points (-3, 2), (2, -3), and (1, 2√3) lie on the circumference of the circle with center at the origin.
d1=√(−3)2+(2)2
d1=√9+4
d1=√13
d2=√(2)2+(−3)2
d2=√4+9
d2=√13
d3=√(1)2+(2√3)2
d3=√1+4⋅3
d3=√1+12
d3=√13
- Distance from the origin to (2, -3) is √13
- Distance from the origin to (1, 2√3) is √13
Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Exercise 7b
18 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Exercise 7c
14 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Problems Of NCERT/exemplar
14 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Long Answer Questions
2 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B
10 Videos
Similar Questions
The points (2k, 3k), (1, 0), (0, 1) and (0, 0) lie on a circle for
View SolutionShow that the points (9, -2), (-5, 12) and (-7, 10) lie on that circle whose centre is the point (1, 4)
View SolutionFind the equation of a circle whose centre is (2,-3) and radius 5.
View SolutionFind the equation of a circle whose centre is (2, 3) and radius is 5.
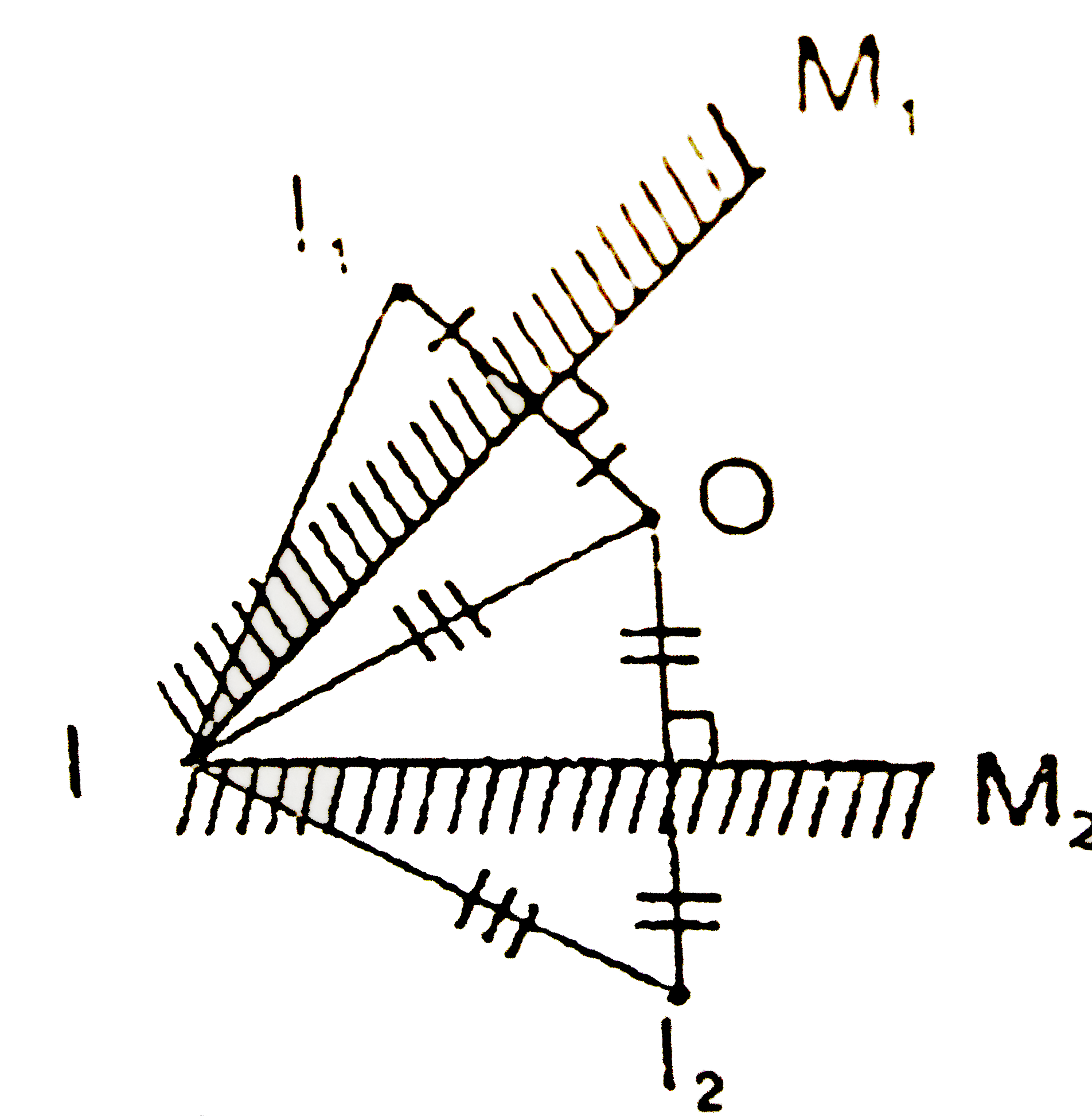
View SolutionFigure shows two inclined plane mirros M1 and M2 and an object O. Its image formed in mirrors M1 and M2 individually and I1 and I2 respectively. Show that I1 and I2 and O lie on the circumference of a circle with centre at I. [This result can be extended to show that all the images will also lie on teh same circle. Note that this result is independent of the angle of inclination of mirrros.]. I is the point of intersection fo the mirrors.
View SolutionShow that the points (3,2,2), (-1,4,2), (0,5,6), (2,1,2) lie on a sphere whose centre is (1,3,4). Find the also its radius.
View SolutionShow that the points A(0,4,3),B(−1,−5,−3),C(−2,−2,1) and D(1,1,1) are coplanar. Also find the equation of the plane in which these points lie.
View SolutionDoes the point (2,5),(3,5) lie inside, outside or on the circle x2+y2=25?
View SolutionShow that the circle x2+y2+4x+4y−1=0 bisects the circumference of the circle x2+y2+2x−3=0 .
View SolutionThe four point of intersection of the lines (2x−y+1)(x−2y+3)=0 with the axes lie on a circle whose center centre is at the point :
View Solution
