For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation
The correct Answer is:1375
To find the mean of the distribution using the empirical relation between the mode, median, and mean, we can follow these steps:
1. Identify the given values:
- Mode (Mo) = 1000
- Median (Me) = 1250
2. Use the empirical relation:
The empirical relation between mode, median, and mean (M) is given by:
3×Median=Mode+2×Mean
Rearranging this relation to find the mean gives:
Mean=3×Median−Mode2
3. Substitute the values into the equation:
Substitute the values of median and mode into the equation:
Mean=3×1250−10002
4. Calculate the numerator:
First, calculate 3×1250:
3×1250=3750
Now substitute this back into the equation:
Mean=3750−10002
5. Perform the subtraction:
Now calculate 3750−1000:
3750−1000=2750
6. Divide by 2:
Finally, divide by 2 to find the mean:
Mean=27502=1375
7. Conclusion:
Thus, the mean of the distribution is:
Mean=1375
Final Answer:
The mean for this distribution is 1375.
- Mode (Mo) = 1000
- Median (Me) = 1250
The empirical relation between mode, median, and mean (M) is given by:
3×Median=Mode+2×Mean
Rearranging this relation to find the mean gives:
Mean=3×Median−Mode2
Substitute the values of median and mode into the equation:
Mean=3×1250−10002
First, calculate 3×1250:
3×1250=3750
Now substitute this back into the equation:
Mean=3750−10002
Now calculate 3750−1000:
3750−1000=2750
Finally, divide by 2 to find the mean:
Mean=27502=1375
Thus, the mean of the distribution is:
Mean=1375
The mean for this distribution is 1375.
Topper's Solved these Questions
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Short Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - EXERCISE 14 E
5 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
Similar Questions
Find the mean for the following distribution :

View SolutionFind the mean for the following distribution :

View SolutionFind mean of the following distribution using short cut method:

View SolutionFind the median for the following distribution :
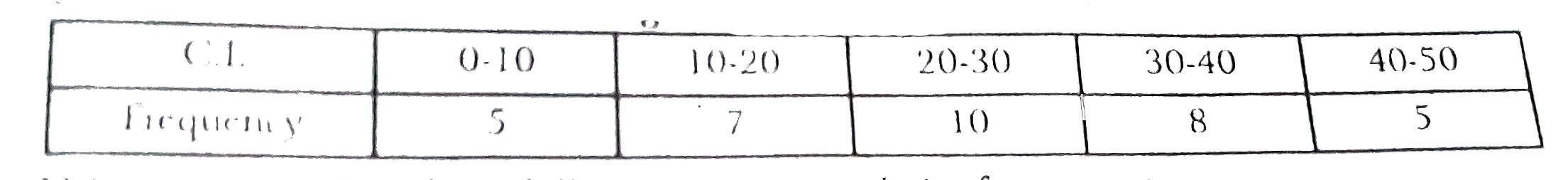
View SolutionFor a slightly asymmetric distribution, mean and medain are 5 and 6, respectively. What is its mode ?
View SolutionFind the mean of the following distribution:
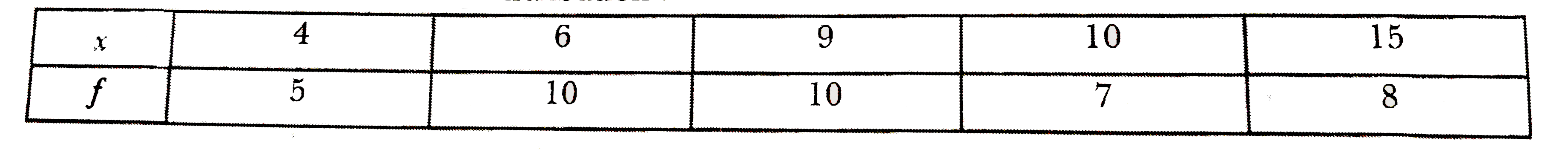
View SolutionFind the mean of the following distribution:

View SolutionFind the mean of the following distribution :

View SolutionIf mode and mean of data are found 28 and 24 respectively, find median using empirical formula.
View SolutionFind the mode for the following distribution.

View Solution
