Two man are on the opposite sides of a tower. They measure the angles of elevation the top of the tower as 30∘ and 60∘. If the height of the tower is 150 m, find the distance between the two men.
To solve the problem, we need to find the distance between two men standing on opposite sides of a tower, given the angles of elevation to the top of the tower and the height of the tower. Let's break down the solution step by step.
Step 1: Understand the Problem
We have a tower of height AD=150 m. Two men are standing at points B and C on opposite sides of the tower. The angle of elevation from point B to the top of the tower A is 60∘, and the angle of elevation from point C to the top of the tower A is 30∘.
Step 2: Set Up the Triangles
We will use right triangle trigonometry to find the distances BD and CD:
- In triangle ABD (where A is the top of the tower, B is the point on the ground near the tower, and D is the foot of the tower):
- tan(60∘)=ADBD
- In triangle ACD:
- tan(30∘)=ADCD
Step 3: Calculate BD (distance from point B to the tower)
Using the tangent function for triangle ABD:
tan(60∘)=√3(since tan(60∘)=√3)
tan(60∘)=ADBD⟹√3=150BD
Rearranging gives:
BD=150√3(let's denote this as x)
Step 4: Calculate CD (distance from point C to the tower)
Using the tangent function for triangle ACD:
tan(30∘)=1√3(since tan(30∘)=1√3)
tan(30∘)=ADCD⟹1√3=150CD
Rearranging gives:
CD=150√3(let's denote this as y)
Step 5: Find the Total Distance Between the Two Men
The total distance BC between the two men is the sum of BD and CD:
BC=BD+CD=x+y=150√3+150√3
Step 6: Simplify the Expression
To combine the terms, we need a common denominator:
BC=150√3+150√3=150+150⋅3√3=150+450√3=600√3
Step 7: Rationalize the Denominator
To rationalize:
BC=600⋅√33=200√3
Final Answer
The distance between the two men is 200√3 meters.
We have a tower of height AD=150 m. Two men are standing at points B and C on opposite sides of the tower. The angle of elevation from point B to the top of the tower A is 60∘, and the angle of elevation from point C to the top of the tower A is 30∘.
We will use right triangle trigonometry to find the distances BD and CD:
- In triangle ABD (where A is the top of the tower, B is the point on the ground near the tower, and D is the foot of the tower):
- tan(60∘)=ADBD
- In triangle ACD:
- tan(30∘)=ADCD
Using the tangent function for triangle ABD:
tan(60∘)=√3(since tan(60∘)=√3)
tan(60∘)=ADBD⟹√3=150BD
Rearranging gives:
BD=150√3(let's denote this as x)
Using the tangent function for triangle ACD:
tan(30∘)=1√3(since tan(30∘)=1√3)
tan(30∘)=ADCD⟹1√3=150CD
Rearranging gives:
CD=150√3(let's denote this as y)
The total distance BC between the two men is the sum of BD and CD:
BC=BD+CD=x+y=150√3+150√3
To combine the terms, we need a common denominator:
BC=150√3+150√3=150+150⋅3√3=150+450√3=600√3
To rationalize:
BC=600⋅√33=200√3
The distance between the two men is 200√3 meters.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise
32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
Similar Questions
Two men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as 45∘ and 30∘ respectively. If the height of the tower is 40 m, then the distance between the men is
View SolutionTwo people standing on the same side of a tower in a straight line with it, measure the angles of elevation of the top of the tower as 25∘and50∘ respectively. If the height of the tower is 70 m, find the distance between the two people
View SolutionThe persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30∘and38∘ respectively. Find the distance between them, if the height of the tower is 50 m
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.

View SolutionTwo points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60∘ and 45∘ respectively. If the height of the tower is 15 m, then find the distance between these points.
View SolutionThe angle of elevation θ of the top of a tower is 30∘. If the height of the tower is doubled, then new tanθ will be
View SolutionAt one side of a road, there os a house and on the other side there is a tower. House and tower are on the same horizontal plane. The angle of depression of the top and foot of the house, from the top of the tower are 30∘ and 45∘ respectively. If the height of the house is 10 m, then find the distance between the house and the tower.
View SolutionOn the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45o and 60o . If the height of the tower is 150m, find the distance between the objects.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
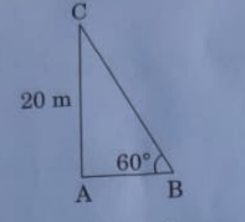
View Solution
