The height and radius of the base of a right circular cylinder is 'r'. Find its totalsurface area.
To find the total surface area of a right circular cylinder where the height and the radius of the base are both equal to 'r', we can follow these steps:
1. Understand the Formula for Total Surface Area of a Cylinder:
The total surface area (TSA) of a right circular cylinder is given by the formula:
TSA=2πr(h+r)
where r is the radius of the base and h is the height of the cylinder.
2. Identify the Given Values:
In this case, both the height h and the radius r of the cylinder are given as r.
3. Substitute the Values into the Formula:
Since both the height and radius are equal to r, we substitute h=r into the TSA formula:
TSA=2πr(r+r)
4. Simplify the Expression:
Now, simplify the expression inside the parentheses:
r+r=2r
So, we can rewrite the TSA formula as:
TSA=2πr(2r)
5. Calculate the Total Surface Area:
Now, multiply the terms:
TSA=4πr2
6. Final Answer:
Therefore, the total surface area of the cylinder is:
TSA=4πr2 cm2
The total surface area (TSA) of a right circular cylinder is given by the formula:
TSA=2πr(h+r)
where r is the radius of the base and h is the height of the cylinder.
In this case, both the height h and the radius r of the cylinder are given as r.
Since both the height and radius are equal to r, we substitute h=r into the TSA formula:
TSA=2πr(r+r)
Now, simplify the expression inside the parentheses:
r+r=2r
So, we can rewrite the TSA formula as:
TSA=2πr(2r)
Now, multiply the terms:
TSA=4πr2
Therefore, the total surface area of the cylinder is:
TSA=4πr2 cm2
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Problems From NCERT/exemplar24videos
SURFACE AREA AND VOLUME
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Exercise 13a30videos
SURFACE AREA AND VOLUME
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise12videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (long Answer Type Question)8videos
TRIANGLES
Similar Questions
The ratio between the radius of the base and the height of a cylinder is 2:3., find the total surface area of the cylinder, it its volume is 1617 cm3.
View SolutionThe ratio between the radius of the base and the height of a cylinder is 2:3., find the total surface area of the cylinder, it its volume is 1617 cm3.
View Solution
Knowledge Check
- Question 1 - Select One
The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
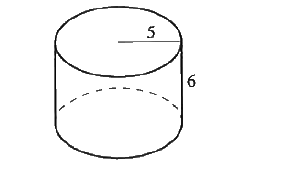 A30πB31πC150πD180π
A30πB31πC150πD180π
The ratio between the radius of the base and the height of a cylinder is 2:3, find the total surface area of the cylinder, it its volume is 1617 cm3
View SolutionThe diameter of the base of a right circular cylinder is 42cm and its height is 10cm. Find the area of the curved surfaces and total surface area.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionThe radii of the bases of a right circular cylinder and a right circular cone are equal. Their vertical heights are 7 cm and 14 cm respectively. Find the ratio of their volumes.
View Solution

