A particle moves in a straight line such that its distance in 't' seconds from a fixed point is (6t−t2) cm. find its velocity at the end of t=2 sec.
To solve the problem, we need to find the velocity of a particle at t=2 seconds, given that its distance from a fixed point is described by the function d(t)=6t−t2 cm.
1. Identify the distance function:
The distance d(t) of the particle at time t is given by:
d(t)=6t−t2
2. Find the velocity function:
The velocity v(t) is the derivative of the distance function with respect to time t:
v(t)=ddt(d(t))=ddt(6t−t2)
3. Differentiate the distance function:
Using the power rule of differentiation:
- The derivative of 6t is 6.
- The derivative of −t2 is −2t.
Thus, the velocity function is:
v(t)=6−2t
4. Evaluate the velocity at t=2 seconds:
Substitute t=2 into the velocity function:
v(2)=6−2(2)=6−4=2
5. State the final answer:
The velocity of the particle at t=2 seconds is:
v(2)=2 cm/s
Summary:
The velocity of the particle at the end of t=2 seconds is 2 cm/s.
The distance d(t) of the particle at time t is given by:
d(t)=6t−t2
The velocity v(t) is the derivative of the distance function with respect to time t:
v(t)=ddt(d(t))=ddt(6t−t2)
Using the power rule of differentiation:
- The derivative of 6t is 6.
- The derivative of −t2 is −2t.
Thus, the velocity function is:
v(t)=6−2t
Substitute t=2 into the velocity function:
v(2)=6−2(2)=6−4=2
The velocity of the particle at t=2 seconds is:
v(2)=2 cm/s
The velocity of the particle at the end of t=2 seconds is 2 cm/s.
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13C
11 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13D
25 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13A
53 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
Similar Questions
A particle is moving in a straight line such that the distance covered by it in t seconds from a point is (t33−t) cm. find its speed at t=3 seconds.
View SolutionA particle moves in a straight line such that its position in 't' time is s(t)=t2+3t−1 cm. find its velocity at t=4 sec.
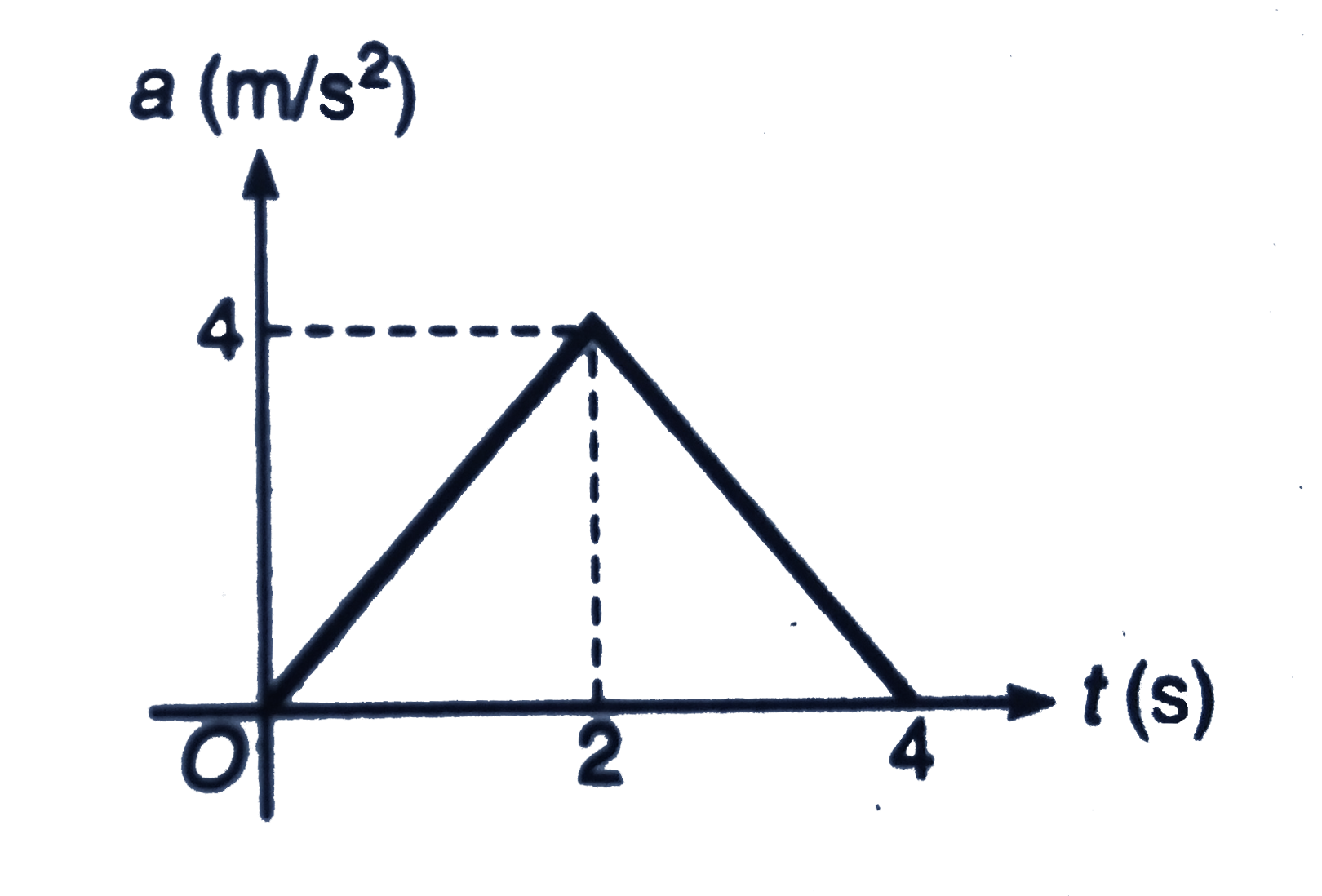
View SolutionAccleration-time graph of a particle moving in a straight line is as shown in Fig. Velocity of particle at time t=0 is 2m/s. Find the velocity at the end of fourth second.
View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum
View SolutionA particle moves along a staight line such that its displacement at any time t is given by s=t3−6t2+3t+4m. Find the velocity when the acceleration is 0.
View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum and acceleration minimum.
View SolutionAcceleration - time graph of a particle moving in a straight line is shown in figure. Velocity of particle at time t = 0 is 2ms−1. Find velocity at the end of fourth second.

View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionThe distance f(t) in metres ived by a particle travelling in a straight line in t seconds is given by f(t)=t2+3t+4. Find the speed of the particle at the end of 2 seconds.
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View Solution
