In figure, if ∠1=∠2 and ΔNSQ=ΔMTR, then prove that ΔPTS~ΔPRQ.
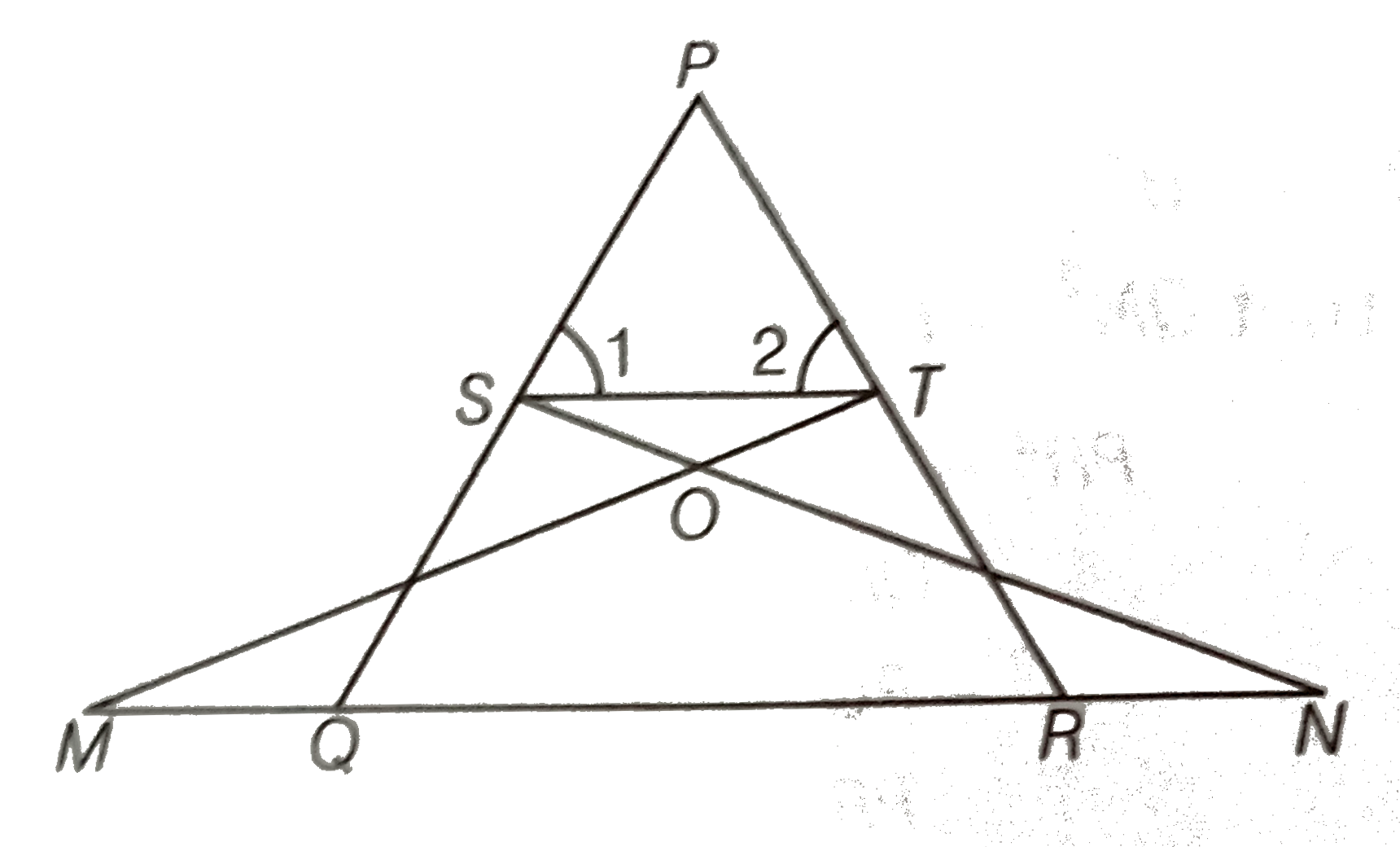
Given: In △PQR points S in on PQ and T is on PR.
such that ∠1=∠2
and △NSQ≅△MTR
To prove : △PTS~△PRQ
Proof : △NSQ≅△MTR ( given)
SQ = TR ( CPCT) ... (1)
∠1=∠2
PT = PS ( sides opposite to equal angles in △PTS) ...(2)
⇒ PTTR=PSSQ [ from (1), (2)]
ST||QR ( by converse of BPT)
Now in ,△PTSand△PRQ ,we have
ST||QR ( prove above)
∠1=∠3 (corresponding angles)
∠2=∠4 ( corresponding angles)
△PTS~△PRQ ( by AA similartiy criterion) Hence proved.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
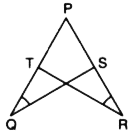
The given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
View SolutionIn the following figure, ∠A=∠C and AB = BC.
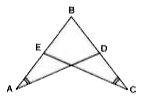
Prove that : ΔABD≅ΔCBE
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
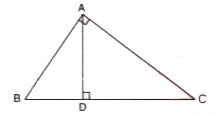
Prove that : ΔABD is similar to ΔCAD.
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.
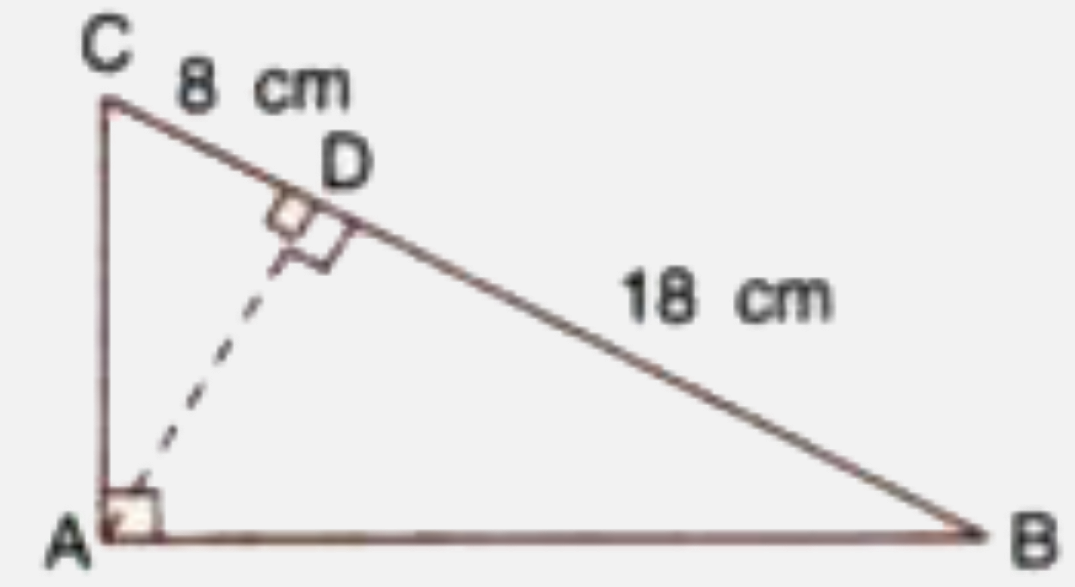
Prove that : ΔADB~ΔCDA.
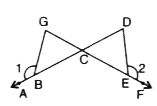
View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
View SolutionIn the adjoining figure, we have ∠1=∠2and=∠3. Show that ∠1=∠3.

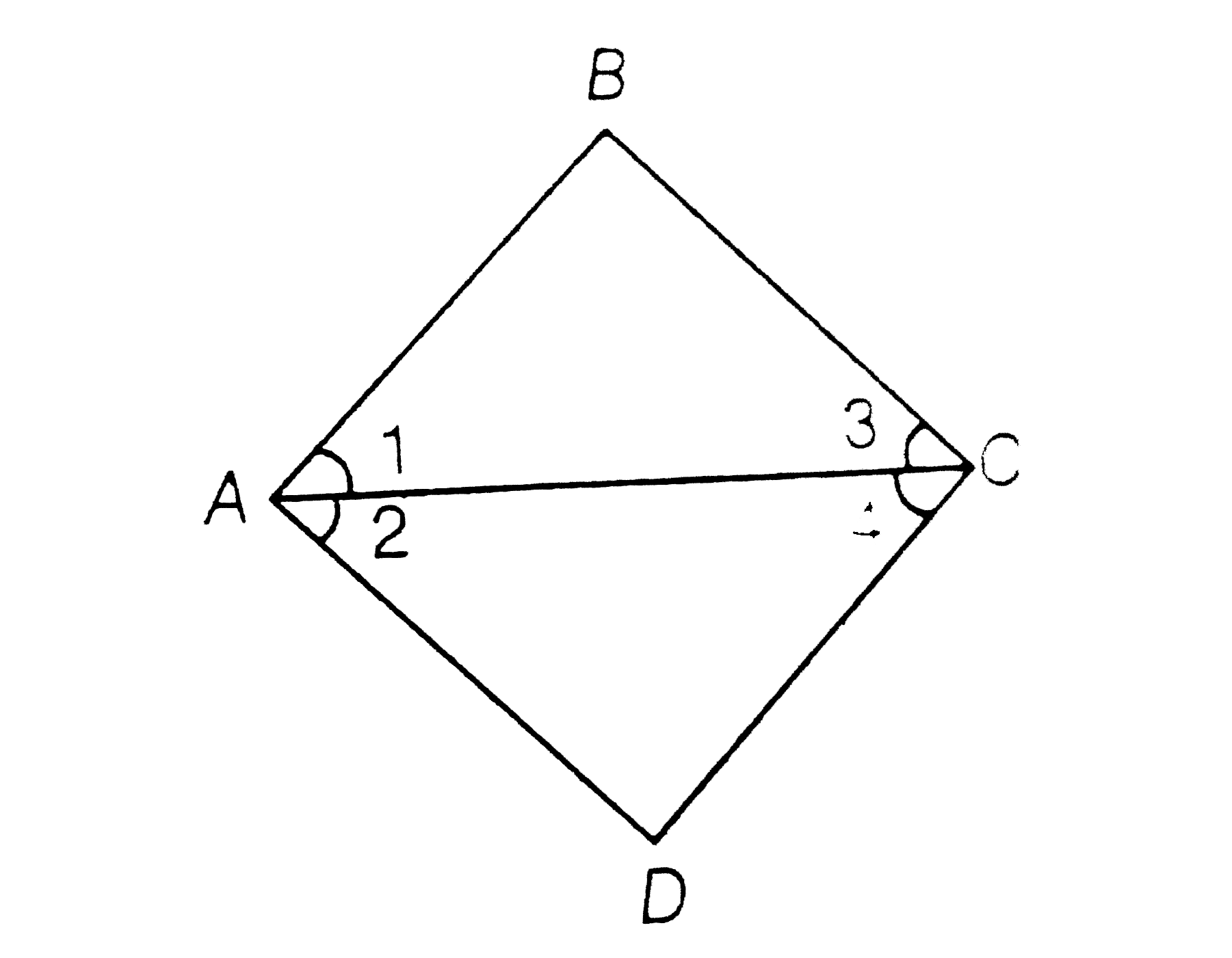
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
View SolutionIn the given figure, AD = DB = DE ∠EAC=∠FACand∠F=90∘
Prove that
(i) ∠AEB=90∘
(ii) ΔCEG is isosceles.
(iii) ∠CEG=∠EAF
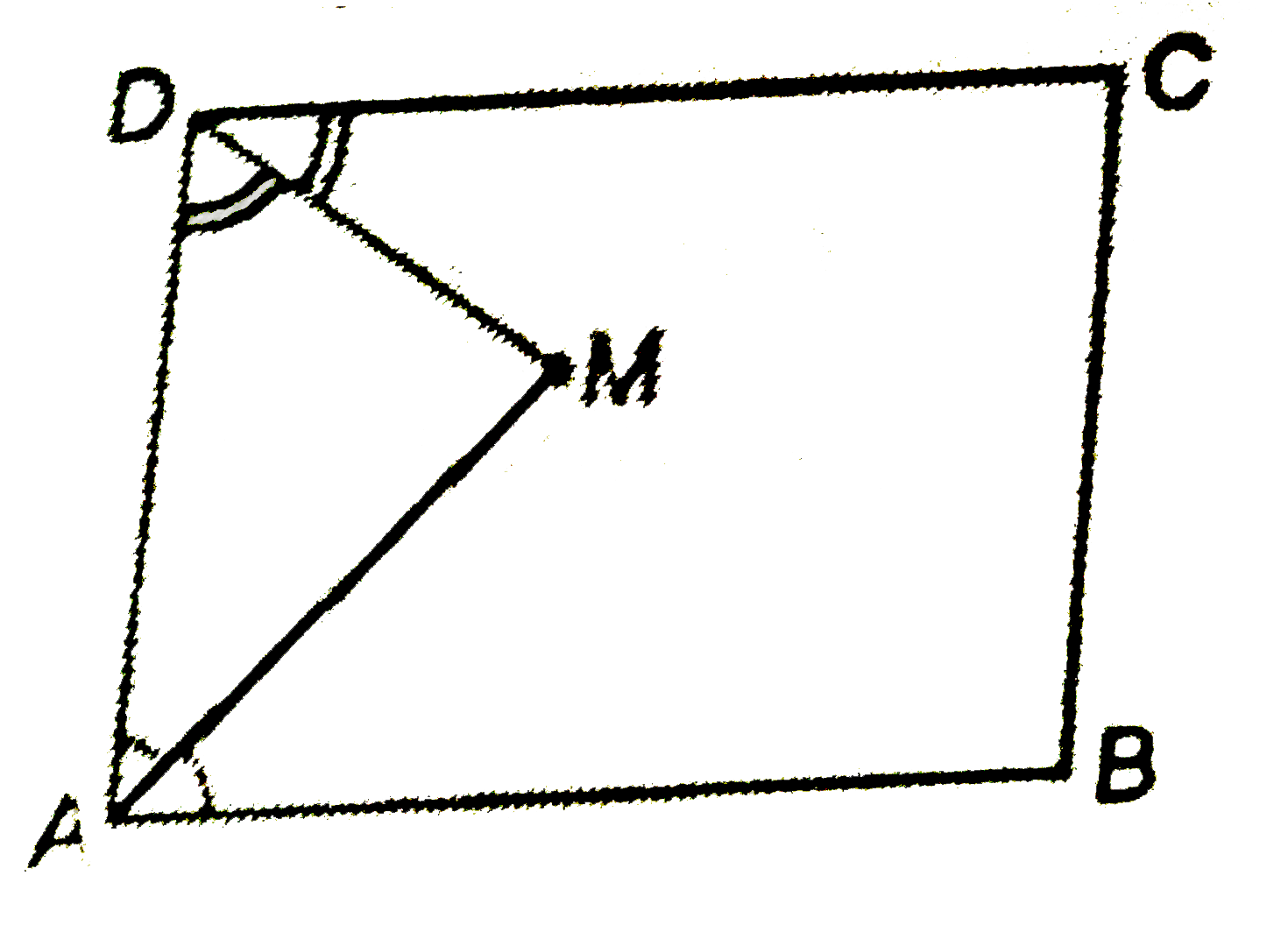
View SolutionIn the given figure, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that ∠AMD=90∘.
View SolutionIn Figure, m∣∣n and angles 1 and 2 are in the ratio 3:2. Determine all the angles from 1 to 8.
View Solution
