Find the which of the operations given above has identity ?
To determine which of the given operations has an identity element, we will analyze each operation step by step.
Step 1: Analyze the first operation a binary b=a−b
1. Definition of Identity Element: An identity element e for a binary operation binary must satisfy the condition:
a binary e=aande binary a=a
for all a.
2. Set up the equations:
- For a binary e=a:
a−e=a
This simplifies to:
−e=0⟹e=0
- For e binary a=a:
e−a=a
This simplifies to:
e=2a
3. Check for uniqueness: From the first equation, we found e=0, but from the second equation, we have e=2a. Since e depends on a, it is not unique. Therefore, there is no identity element for this operation.
Conclusion for the first operation:
The identity element does not exist for the operation a binary b=a−b.
---
Step 2: Analyze the second operation a binary b=a2+b2
1. Definition of Identity Element: Again, we need to find e such that:
a binary e=aande binary a=a
2. Set up the equations:
- For a binary e=a:
a2+e2=a
Rearranging gives:
e2=a−a2
- For e binary a=a:
e2+a2=a
Rearranging gives:
e2=a−a2
3. Check for values of e:
- The equations e2=a−a2 must hold for all a.
- If we take specific values, for example:
- If a=0, then e2=0−02=0 implies e=0.
- If a=1, then e2=1−12=0 implies e=0.
- If a=2, then e2=2−22=−2, which does not yield a real number for e.
4. Conclusion for the second operation: Since e2 cannot be negative for real numbers, we conclude that there is no identity element for the operation a binary b=a2+b2.
Final Conclusion:
The identity element does not exist for the operation a binary b=a2+b2.
---
Summary of Results:
- For a binary b=a−b: No identity element exists.
- For a binary b=a2+b2: No identity element exists.
a binary e=aande binary a=a
for all a.
- For a binary e=a:
a−e=a
This simplifies to:
−e=0⟹e=0
e−a=a
This simplifies to:
e=2a
The identity element does not exist for the operation a binary b=a−b.
a binary e=aande binary a=a
- For a binary e=a:
a2+e2=a
Rearranging gives:
e2=a−a2
e2+a2=a
Rearranging gives:
e2=a−a2
- The equations e2=a−a2 must hold for all a.
- If we take specific values, for example:
- If a=0, then e2=0−02=0 implies e=0.
- If a=1, then e2=1−12=0 implies e=0.
- If a=2, then e2=2−22=−2, which does not yield a real number for e.
The identity element does not exist for the operation a binary b=a2+b2.
- For a binary b=a−b: No identity element exists.
- For a binary b=a2+b2: No identity element exists.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise19videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Exercise 1.314videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise19videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Miscellaneous Exercise23videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Show that none of the operations given below has identity.(i) a∗b=a−b (ii) a∗b=a2+b2 (iii) a∗b=a+ab (iv) a∗b=(a−b)2 (v) a∗b=ab4 (vi) a∗b=ab2
View SolutionLet ∗ be a binary operation on the set Q of rational numbers as follows:
(i) a∗b=a−b (ii) a∗b=a2+b2
Find which of the binary operations are commutative and which are associativeView SolutionFind the identity element for the binary operation * on Z defined as a*b = a + b-5. Also find the inverse element of 100.
View SolutionFind the total number of binary operations on {a, b} .
View Solution
In the figure above, the circle with center O has ¯¯¯¯¯¯PQ tangent to it at P. Find the ratio of the shaded area to the area of the circle .View SolutionFind the identity and invertible elements in Z of the binary operation * defined as a * b = a + b-4, ∀a,b∈Z.
View SolutionShow that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations −:R×R→Rand ÷:R⋅×R⋅→R⋅.
View SolutionGiven the circuit :
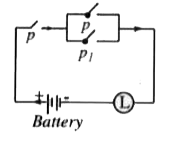
Which of the following is equivalent to the above circuit ?
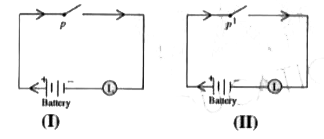
The true statement in the above is/areView Solution_2019_CBT5_E01_057_Q01.png)
Which of the above is inconsistent for the given meter bridgeView SolutionFind the equation of the line which satisfy the given conditions : Intersecting the yaxis at a distance of 2 units above the origin and making an angle of 30∘with positive direction of the xaxis.
View Solution

