Question

Establish the following vector inequalities geometrically or otherwise :
$|a-b|\le \left|a\right|+\left|b\right|$
When does the equality sign above apply ?

Explanation

Consider two vectors `vec(A)` and `vec(B)` be represented by the sides `vec(OP)` and `vec(OQ)` of a parallelogram OSPQ. According to parallelogram law of vector addition, `(vec(A) + vec(B))` will represented by `vec(OS)` as shown in figure. Thus `OP = |vec(A)|, OQ = PS = |vec(B)|` and `OS = |vec(A) + vec(B)|`

To prove `|vec(A) - vec(B)| le |vec(A) + vec(B)|`
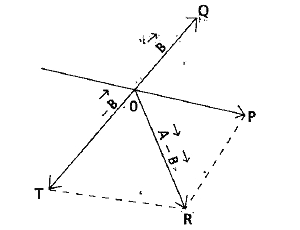
`vec(A) = (vec(OP))` and `-vec(B) = vec(OT) = vec(PR)` and `(vec(A) - vec(B)) = vec(OR)`
From `Delta ORP` we note that `OR lt OP + PR` or `|vec(A) - vec(B)| lt |vec(A)| + -|vec(B)|` or `|vec(A) - vec(B)| lt |vec(A)| + |vec(B)|` ...(vi)
If two vectors are acting along a straight line but in opposite direction, then `|vec(A) - vec(B)| = |vec(A)| + |vec(B)|` ...(vii)
combining the conditions mentioned in (vi) and (vii) we get
`|vec(A) - vec(B)| le |vec(A)| + |vec(B)|`