Question

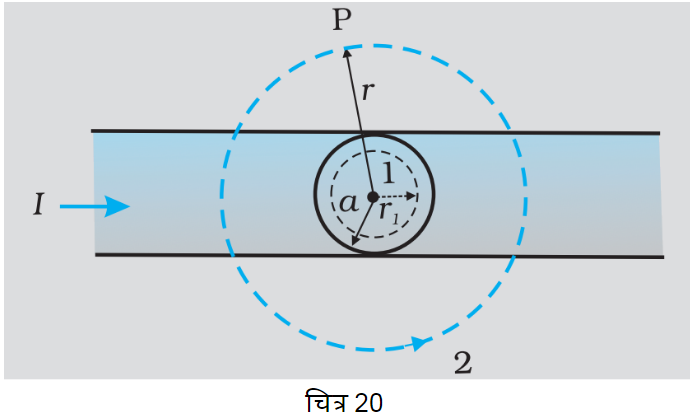
चित्र 20 में एक लंबा सीधा वृत्ताकार अनुप्रस्थ काट का (जिसकी त्रिज्या a है) विद्युत धारावाही तार जिससे स्थायी विद्युत धारा $I$ प्रवाहित हो रही हो, दर्शाया गया है। स्थायी विद्युत धारा इस अनुप्रस्थ काट पर एकसमान रूप से वितरित है। क्षेत्रों $r<a$ तथा $r>a$ में चुंबकीय क्षेत्र परिकलित कीजिए

Explanation

(a) प्रकरण `r gt a` पर विचार कीजिए। जिस पाश पर 2 अंकित है वह अनुप्रस्थ काट के साथ संकेंद्री वृत्त के रूप में एम्पियर पाश है। इस पाश के लिए
`L = 2pir`

`I_e =` पाश द्वारा परिबद्ध विद्युत धारा = `I`
यह परिणाम किसी सीधे लंबे तार के लिए सुपरिचित व्यंजक है।

`B (2π r) = µ_0 I`

`B=(mu_0 I)/(2pir)`

`B prop 1/r` `(r gt a)`
(b) प्रकरण `r lt a` पर विचार कीजिए। इसके लिए ऐम्पियर पाश वह वृत्त है जिस पर 1 अंकित है।
इस पाश के लिए वृत्त की त्रिज्या r लेने पर,

`L = 2 π r`
अब यहाँ परिबद्ध विद्युत धारा `I_e` का मान `I` नहीं है परतु यह इस मान से कम है। चूँकि विद्युत धारा का विवरण एकसमान है, परिबद्ध विद्युत धारा के अंश का मान

`I_e=I((pi r^2)/(pi a^2))=(Ir^2)/a^2`
ऐम्पियर के नियम का उपयोग करने पर

`B(2pir)=mu_0 (Ir^2)/a^2`

`B = ((mu_0I)/(2pia^2))r`

`B prop r (r lt a)`

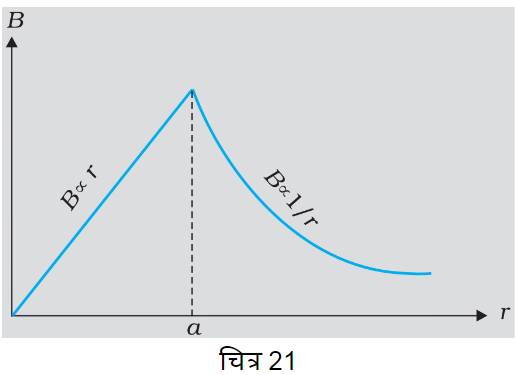
चित्र (21) में `vecB` के परिमाण तथा तार के केंद्र से दूरी r के बीच ग्राफ दर्शाया गया है। चुंबकीय क्षेत्र की दिशा अपने अपने वृत्ताकार पाशों (1 अथवा 2) के स्पर्शरेखीय है तथा यह दक्षिण हस्त नियम से निर्धारित की गई है। इस उदाहरण में आवश्यक सममिति विद्यमान है इसलिए इसी पर ऐम्पियर का नियम आसानी से लागू किया जा सकता है।