A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. Show that AQ = 1/2(Perimeter of ΔABC).

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for A circle touches the side BC of a DeltaABC at a point P and touches AB and AC when produced at Q and R respectively. Show that AQ = 1/2(Perimeter of DeltaABC). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023
Class 10MATHSMODEL QUESTION PAPER -2 [UNSOLVED]

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A circle touches the side BC of a ΔABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of ΔABC = 26.4 cm, then the length of AQ is:

    A8.8 cm
    B13.2 cm
    C15.4 cm
    D17.6 cm

  • In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
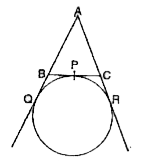    ocr_image

    AOne-third of the perimeter of Δ ABC.
    BHalf of the perimeter of Δ ABC.
    CTwo-third of the perimeter of Δ ABC
    DThree-fourth of the perimeter of Δ ABC

  • A circle touches the side BC of ΔABC at D and AB and aC are produced to E and F, respectively. If AB=10cm, AC=8.6 cm and BC=6.4 cm then BE=?

    A3.5cm
    B3.2cm
    C2.5cm
    D2.2cm